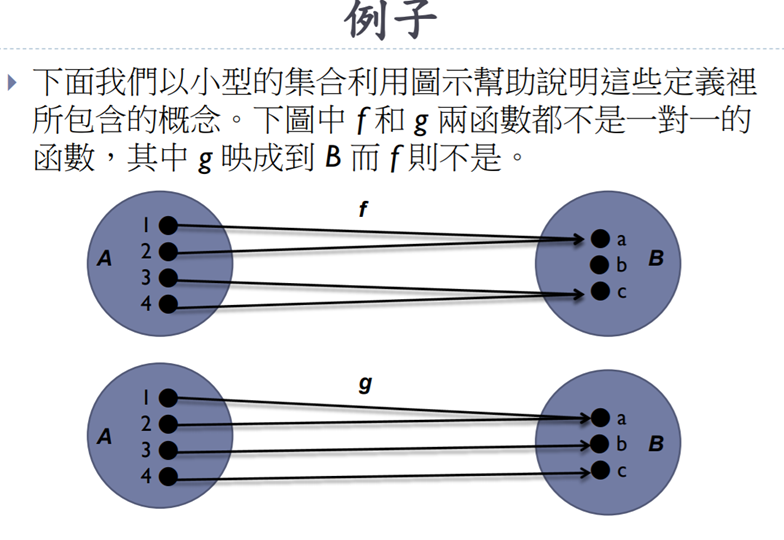
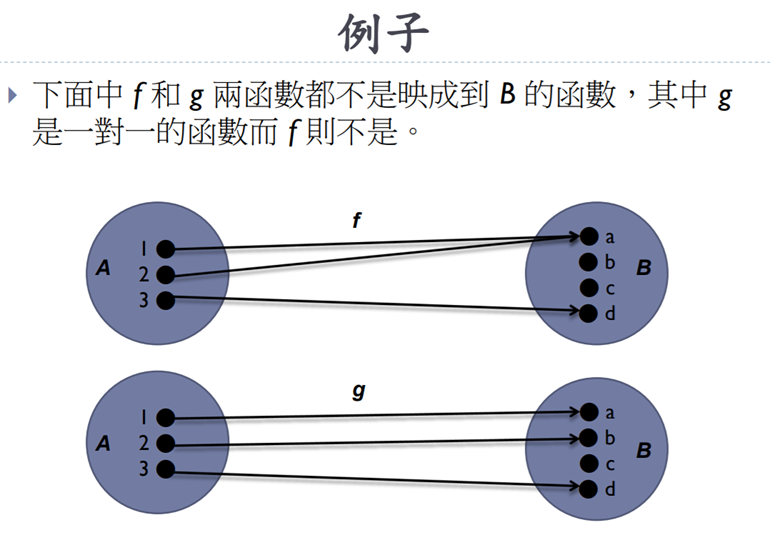
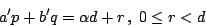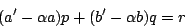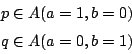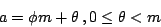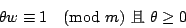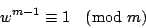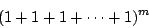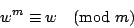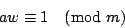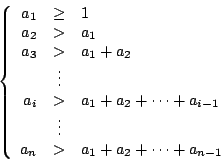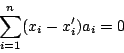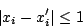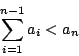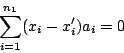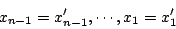數論在密碼上的應用

有限體在密碼學日漸益重要，許多密碼學演算法，都很依賴有限體的特性，尤其是進階加密標準(AES)和橢圓曲線密碼學。

群(groups)、環(rings)、和體(fields)是抽象代數或現代代數的基本要素。

在抽象代數中，我們關心的是哪些集合元素可以代數運算。

抽象代數：研究對象是 Algebra Structure(代數結構)。(把它想成集合 + 一套運算規則)

相關概念：

Arithmetic(算數)：(最大特點=>關注在具體數字上)
- 數學中最古老、最基礎的部分。
- 研究數的性質和其運算。(性質：如算法對象為自然數、整數、有理數、實數；運算：不僅僅是+ - \* /也可以是% log。)
Elementary Algebra(初等代數)：
- 用符號(變數)代表具體數字，就可得到更一般化(generalization)的等式，如：(2+3)^2 = 2^2+2*2*3+3^2。
- Arithmetic累積了大量數量問題的解法，為了尋求更系統、更普遍求解就產生了「以解方程式為中心」的初等代數。
Abstract Algebra(抽象代數)：(將初等代數再更進一步一般化)
- Galois是現代群論創始人，利用Galois理論的概念徹底解決了用「根式求解代數方程」的可能性問題。 Galois理論：解釋了為何5次以上方程式無公式解，而以下有。「代數學」從解方程式的科學轉變為研究代數結構的科學。 (從代數推廣為抽象代數)
- 主要研究對象是代數結構：群、環、體、向量空間。
Linear Algebra(線性代數)：為抽象代數特殊的一類，其代數結構為「Vector Space + Linear Mapping」。

初等代數與抽象代數的界線在於：初等代數只考慮「實數」和「複數」的代數結構。

初等代數 -------> 抽象代數

數 => 集合(set)：
- naive set theory：定義了集合是由一些元素組成。
- axiomatic set theory：定義了集合是具有某種特質的元素總稱。
加減 => 二元運算(Binary Operation)：當集合中兩元素做binary operation得到的新元素仍屬該集合稱「對稱姓」(Closure)。
0/1 => 單位元素(Identity Elements)：0為加法單位元素，1為乘法單位元素。單位元素是集合內的一個特殊元素(與binary search有關)，取決於元素與二元運算。如matrix加法單位元素是「零矩陣」，乘法單位元素是「單位矩陣」。

負數 => 反元素(Inverse Element)：對於加法 --> a的反元素-a。

                                                       對於乘法 --&gt; a的反元素a^-1\(1/a\)。

結合律(Associative property)：是某些binary operation的性質，有些則沒有(如減法和除法)。(a*b)*c=a*(b*c)
交換律(Commutative property)：是某些binary operation的性質，有些則沒有(如矩陣乘法)。a*b=b*a

群(Group)：

一個代數結構(G, ·)，二元運算 " · " 根據：

closure
identity elements
inverse elements
associative property
commutative property

可歸納成不同的Group。

(G, ·) -----封閉性-----> 原群(magma) -----結合律-----> 半群(semigroup) -----單位元素-----> 么半群(monoid) -----反元素-----> 群(group) -----交換律-----> 阿貝爾群 /交換群(Abelian group)。

群公理(group axioms)：封閉性、結合律、單位元素、反元素。

群(group)的例子：整數加法 (Z, +)。

環(Ring)：

一個代數結構(R, + , ·)，須滿足環公理(ring axioms)，如整數加法和乘法(Z, + , x)。

(+, · 兩種二元運算常被簡稱為加法和乘法，但與一般所說的加法和乘法不同)

環公理：(R, +)是交換群，(R, ·)是么半群-->乘法單位元素為1 (a·1=a and 1·a=a)，以及乘法對加法滿足分配律。

(R, + , ·) 需滿足：

(R, +) -----封閉性-----> 原群(magma) -----結合律-----> 半群(semigroup) -----單位元素-----> 么半群(monoid) -----反元素-----> 群(group) -----交換律-----> 阿貝爾群 /交換群(Abelian group) -----乘法對加法有分配律----->環(Ring)。
(R, ·) -----封閉性-----> 原群(magma) -----結合律-----> 半群(semigroup) -----單位元素-----> 么半群(monoid) ---------->環(Ring)。

交換環：若環R中，(R, ·)還滿足交換律，即：∀a，b∈R，有ab=ba，則R稱為交換環。

整環(Integral domain)：沒有「零因子」的交換環。如整數環 (Z, +, x)。

假設(R, + , ·)為交換環，e∈R, e!=0，∀a∈R, a·e=e·a=a (存在乘法反元素) ∀(a,b)∈R^2, a·b=0 => a=0 V b=0 (沒有零因子)

多項式環：一個環R上的多項式環，是由系數在R中的多項式構成的環，其中的代數運算由多項式的乘法與加法定義。

體(Field)：

一個代數結構(F, + , ·)，須滿足(F, + , ·)為交換環以及每個非零元素都有乘法反元素。

在交換環(Commutative Ring)基礎下還增加了「除法」二元運算，要求非零元素可作除法運算，即「每個非零元素都有乘法反元素」。體是可以進行+-/*的代數結構。整數Z集合不存在乘法反元素，所以Z不是Field。

模數運算：

若a為整數、n為正整數，將a mod n的值定義為a除n的餘數，整數n稱為模數。
若(a mod n)=(b mod n)：整數a、b是n的同餘，寫成a ≡ b (mod n)。
若n|(a - b)，則a ≡ b (mod n)。
若a ≡ b(mod n)，則b ≡ a (mod n)。
若a ≡ b(mod n) 且 b ≡ c (mod n)，則a ≡ c (mod n)。
a ≡ b (mod n)，而所以與a同餘的整數所形成的集合，即[a]={ b∈Z | a ≡ b(mod n) }，稱之為a的同餘類。
所有(mod n)同餘類所形成的集合，即Z/n(或寫成Zn)={ [x]|x∈Z }，如：Z/3={ [0],[1],[2] }。
模加法：表示在某個領域(或稱 mod n )內執行加法運算。基本上，參與計算數值的大小應該不會超過該領域，計算後的結果也不會超過該領域(mod n)。
- [(a mod n) + (b mod n)] mod n = (a + b) mod n。
- 反函數/反向暗門(Inverse Backdoor)/陷門函數(Trapdoor Function)：假設將一個數值a經過某種演算法運算後得到數值b，如果現在找到一個方法，可以透過某個數值c與b反推出a的值，則c稱為a的反函數/反向暗門。
- 模加法是否具有反函數/反向暗門(Inverse Backdoor)的功能。假設以mod 10為例，而明文、公開金鑰、私有金鑰、以及密文都介於0 ~ 9之間，其中公開金鑰KU與私有金鑰KR之間的關係是 KU+KR ≡ 0 (mod 10)，且加密與解密演算法都是模加法運算 (mod 10)。
  
  範例：KU= 4、KR= 6、明文P=5，則利用公開金鑰加密得密文C = KU+5 = 4+5 ≡ 9 (mod 10)，再利用私有金鑰解密，還原明文為P = KR+ 9 = 6+9 ≡ 5 (mod 10)。
- 因此，可以做一個簡單的結論，模加法具有反函數的能力，又稱之為「加法反向」(Addition Reverse)。假設模數為n，任何數值y，與其加法反元素為y^-1，如果滿足「反函數」，則兩數之間的關係為：y + y^-1≡0 (mod n)。
模乘法：概念如同加法一樣，在某一領域內(mod n)執行乘法運算。基本上，運算元與運算結果都不會超過其領域。
- [(a mod n) × (b mod n)] mod n = (a × b) mod n。
- 利用模乘法所推演出來的反函數，稱之為「乘法反向」(Multiplicative Reverse)。設模數為n，任何數值y，與其乘法反元素為y^-1，如果滿足「乘法反向」，則兩數之間的關係為：y × y^-1≡1 (mod n) (0 < y < n；0 < y-1< n；y或y^-1必須與n互質)。
模指數：在某領域內(mod n)執行指數運算。基本上，參與運算元與結果的大小都不會超過該領域。指數運算不需較大的數值參與運算，就可能產生非常大的運算量，沒經過特殊方法運算，幾乎很難完成指數運算(RSA主要運算方法）。
- (a mod n)^b mod n = (a^b) mod n。
- 其實指數運算表示自我函數相乘的次數，如X^3表示X自我相乘3次。模指數是模乘法運算的延伸，它的反函數也與模乘法相同，如下：y×y^-1≡1 mod n。

有限體(Galois Field)：

有限體是加密的關鍵角色。
我們可以證明有限體的級數(元素數目)必須是質數的乘冪，也就是p^n(n為正整數)。
級數p^n的有限體通常以GF(p^n)表示或Fp^n。
對質數p而言，級數(Order)p的有限體GF(p)定義成：整數集合Z/p={0, 1,…,p-1}，以及算術運算模數p，所形成的有限體。

以GF(7)為範例：

GF(7) = Z/7 = {0,1,2,3,4,5,6}

a + b => (a+b) (mod 7)

a * b => (a*b) (mod 7)

a的加法反元素a^-1滿足a + a^-1 = 0。 ex: 3 - 4 = 3 + 4^-1 = 3 + 3 = 0

a的乘法反元素a^-1滿足a * a^-1 = 1。 ex: 3^-1 = 5
不能選擇合數來建立新的運算規則。

例如：GF(6) = {0,1,2,3,4,5}，其中2是6的因數，它沒有乘法反元素，也就是2乘上1~5任何一數在mod 6的世界都不會是1。
GF(2) = {0,1} -----> anx^n + .... + a2x^2 + a1x^1 + a0，其中ai∈GF(2)。

多項式的四則運算是基於它的係數的四則運算建立，而係數是遵循GF(2)的規則。

例如：(x+1)+1=x (因為1 + 1=0)

(x+1)(x+1)=x(x+1)+x(x+1)=x^2+x+x+1=x^2+1
體擴張(Field Extension)：從GF(2)擴張到GF(2^n)

在「現有體為係數的多項式」中，找到一個最高次數為n的質/不可約多項式(Prime-Polynomial)，再將所有多項式模它，所得結果之集合。
在AES中所用到之Galois體GF(2^8)，並非直接由整數Z作模運算可得。其中一種典型作法是先考慮多項環：

F2[x] := { f(x)=anx^n + .... + a2x^2+a1x+a0|某n∈N， ai∈GF(2)}，

在進行模運算 (mod x^8+x^4+x^3+x+1)。

當中x^8+x^4+x^3+x+1為首相係數為1之質/不可約GF(2)多項式。

GF(p)[x] / (l(x)) (其中l(x)為首相係數為1之不可約多項式)：代表所有GF(p)多項式模l(x)之同餘類所形成之集合。
AES中所用到之Galois體GF(2^8) ≈ GF(2)[x] / P(x)，其中P(x)=x^8+x^4+x^3+x+1。

其元素可以很自然地化為2進位數，GF(2)多項式之加法即XOR運算，乘上x即左移一位元，末位填0。

同餘式的相關簡單定理、費馬小定理、尤拉函數、尤拉定理：

定理1：

若 p ≡ q (mod m)，a ≡ b (mod m)，則 ap ≡ bq (mod m)。

定理2：

若兩正整數p,q互質，則可以找到二整數(不一定正)a,b，使得 ap+bq=1。

證明：

令A為包含所有x=ap+bq>0，a,b為整數之集合，A集合顯然不是空集合，因可取a=b=1, p+q>0。

令d為此集合中之最小者，若d=1，則本定理得證，若d>1，令 ap+bq=d>1，則任取此集中之另一數。a'p+b'q，則我們若以d除a'p+b'q，則得

$\begin{displaymath} a'p+b'q = \alpha d+r \, , \; 0\leq r<d \end{displaymath}$

代入 d=ap+bq

則得

$\begin{displaymath}$a'-\alpha a$p+$b'-\alpha b$q=r\end{displaymath}$

此r必為0，否則r為A集合中一小於d之數，與假設d為最小數相矛盾，因r=0，故d為A集中任何一數之因數。因

$\begin{displaymath} \begin{eqalign} p & \in A$a=1,b=0$ \\ q & \in A$a=0,b=1$ \end{eqalign}\end{displaymath}$

故d為p，q之公因數。但p，q之最大公因數為1，故d=1，定理證畢。

系理1：

若w與m為二互質的正整數且m>w，則可找到一正整數θ使得 wθ ≡ 1 (mod m)。

由定理知，有a、b二整數使得aw+bm=1，因bm為m之倍數，故 aw ≡ 1 (mod m)

令

$\begin{displaymath}a=\phi m+\theta\, , 0\leq \theta <m\end{displaymath}$

則得

$\begin{displaymath} \theta w \equiv 1 \pmod{m} \mbox{ {\fontfamily{cwM0}\fontseries{m}\selectfont \char 47} } \theta\geq 0 \end{displaymath}$

因θ不可能為0，故本系得證。

費馬小定理：

若m為質數，w為任一與m互質之整數，則

$\begin{displaymath} w^{m-1} \equiv 1 \pmod{m} \end{displaymath}$

證明：

先把w寫成w個1的和，則由多項式定理知

$\begin{displaymath}$1+1+1+\cdots +1$^m\end{displaymath}$

之展開式中除w個1之外，都含有m之因數，(m為質數m!中之m不可能消去)，故

$\begin{displaymath} w^m\equiv w \pmod{m} \end{displaymath}$

兩邊乘以a，即

$\begin{displaymath} aw\equiv 1 \pmod{m} \end{displaymath}$

得

$\begin{displaymath} w^{m-1} \equiv 1 \pmod{m} \end{displaymath}$

本定理證畢。

Euler’s Totient函數 ψ(n)：

是公開金鑰演算法中重要的參數，其意思是小於n但與n互質之正整數的數目，譬如ψ(10) = 4，因為小於10且與10互質的正整數共有4個(1, 3, 7, 9)。

n ψ(n) n ψ(n) n ψ(n)

1 1 11 10 21 12

2 1 12 4 22 10

3 2 13 12 23 22

4 2 14 6 24 8

5 4 15 8 25 20

6 2 16 8 26 12

7 6 17 16 27 18

8 4 18 6 28 12

9 6 19 18 29 28

10 4 20 8 30 8

如果p為質數的話，則：ψ(p) = p-1。如，p=3，則ψ(3) = 3-1=2、p=19，則ψ(19) = 18。

現在假設有兩個質數p與q，且n = pq，則：ψ(n) =ψ(pq) =ψ(p)×ψ(q) = (p-1)×(q-1)。

n	ψ(n)	n	ψ(n)	n	ψ(n)
1	1	11	10	21	12
2	1	12	4	22	10
3	2	13	12	23	22
4	2	14	6	24	8
5	4	15	8	25	20
6	2	16	8	26	12
7	6	17	16	27	18
8	4	18	6	28	12
9	6	19	18	29	28
10	4	20	8	30	8

Euler 定理：

如果a與n互質，則 a^ψ(n) ≡ 1 (mod n)。

例如：a=3, n=10，則ψ(10)=4 => 3^4=81 ≡ 1 (mod 10)。

定理3：

令 (a1,a2,…,an) 為一含n個正整數的數列，並滿足

$\begin{displaymath}\left\{ \begin{array}{rcl} a\_1&\geq&1 a\_2&>&a\_1 a\_3&>... ...dots& a\_n&>&a\_1+a\_2+\cdots +a\_{n-1} \end{array}\right. \end{displaymath}$

又令 (x1,x2,…,xn) 為一由0與1組成的數列，即所有的xi不是0就是1，現假設a1，a2，…，an為已知，x1，x2，…，xn為未知，c為一正整數，則方程式

$\begin{displaymath} c=\sum\_{i=1}^n a\_ix\_i \eqno{$2.2$} \end{displaymath}$

只有一解或無解。

證明：

設此方程式有二解 (x1,x2,…,xn) 及 (x'1,x'2,,…,x'n) 則消去c之後可得

$\begin{displaymath}\sum\_{i=1}^n $x\_i-x\_i'$a\_i=0\end{displaymath}$

又因為

$\begin{displaymath}\vert x\_i-x\_i'\vert\leq 1 \end{displaymath}$

且

$\begin{displaymath}\sum\_{i=1}^{n-1} a\_i<a\_n\end{displaymath}$

故an之係數必為0，即xn=xn'，因此

$\begin{displaymath}\sum\_{i=1}^{n\_1} $x\_i-x\_i'$a\_i=0\end{displaymath}$

同理可得

$\begin{displaymath}x\_{n-1}=x\_{n-1}',\cdots ,x\_1=x\_1'\end{displaymath}$

此兩解原為一。本定理得證。