公開金鑰密碼系統
為何要使用公開金鑰密碼?在AES開始使用以來,對稱式金鑰密碼所能提供的安全度,甚至比一般的長度的RSA還要強;另一方面,對稱式金鑰密碼運算速度快速,適用於大批資料加密,然而卻在金鑰分配與金鑰管理上,衍生了相當麻煩的問題。
例如:當Alice與Bob想要使用「對稱式金鑰密碼」加解密,必定是先利用安全管道來協定所用之密鑰;當人數龐大時,假設有n個人,此時就要有n(n-1)/2=Cn取2串不同的密鑰。在一個中型機構,假設有5000人,此時就要有C5000取2=12497500把不同密鑰,而每人就要保存4999把不同密鑰,這在管理、成本考量有諸多不便。
反觀,公開金鑰密碼系統,每人各有一對金鑰,即一把公鑰以及一把私鑰,其中公鑰公開而私鑰保密,任何使用者均可在公布之公鑰目錄上,查到所要通訊者之公鑰。
這在金鑰數目上,便可將原先對稱式金鑰密碼n(n-1)/2降至2n,而使用者只需保管好自己的私鑰。
1970年代可說是密碼學百花齊放的年代,密碼學領域裡出現三組偉大的開啟者。
- 首先是Feistel於1973提出的乘積與重複編碼技巧,不但開啟區塊加密編碼的大門,今日大部分對稱式加密系統還是沿用此架構。
- 接著Diffie與Hellman於1976年提出金鑰交換的基本架構,仍是目前各種金鑰交換協定主要的基礎。此外,他們又提出一個單向陷門函數(Trapdoor One-Way Function)密碼學的基本架構和「數位簽章」(Digital Signature)的概念,只是當時他們並不知道單向陷門是否真的存在。
- 到了1978年,才由美國麻省理工學院(MIT)三位先進(Rivest、Shamir與Adleman)率先提出一個藉由分解因數之指數函數作為單向陷門的函數,從此開啟了公開鑰匙密碼系統(Public Key Cryptosystem)的序幕。
「公開金鑰密碼學」與「對稱式金鑰密碼學」是截然不同的演算法。對稱式金鑰密碼學是利用取代與置換的技巧來達成加密編碼的功能,然而公開金鑰密碼學完全不再採用取代與重排的技巧,而是依照「數論」(Number Theory)原理所發展出來。
在一公開金鑰密碼系統中,任何使用者可以取得其他使用者的公鑰,假設Alice想要加密一段重要訊息與Bob通訊,她在目錄上找到Bob之公鑰,透過加密函數EBob(‧)將訊息加密成密文傳給Bob,Bob收到密文後便可透過自己的私鑰,用解密函數DBob(‧)解密。在這些步驟中有以下特性:
- 將一已加密的訊息m解密,即可還原成m,即 DBob(EBob(m))=m。
- 加解密函數EBob(‧)、DBob(‧)必須式容易計算的。
- 公開的加密函數EBob(‧),並不會提供任何簡易計算解密函數DBob(‧)的方法,在實用上,這意味者只有Bob才能將任何經加密函數EBob(‧)之訊息有效地解密,也只有Bob知道「陷門」(Trapdoor)才能有效計算DBob(‧)。
- 若將任何訊息m先用解密函數DBob(‧)作用,在作用加密函數EBob(‧),亦可還原成m,即 EBob(DBob(m))=m。
單向陷門函數(Trapdoor One-Way Function)定義:函數EBob(‧)若滿足性質1、2、3就稱之。若性質1、2、3、4皆滿足,就稱為單向陷門置換(Trapdoor One-Way Permutation)。
公開金鑰密碼系統的實踐需要單向陷門函數(Trapdoor One-Way Function),雖然Diffie和Hellman已提到此概念,但卻未能提出任何有關之實例。單向陷門函數之所以稱為「單向」,就是如此之函數可以輕易地計算一個方向;但另一個方向卻是非常難計算的。
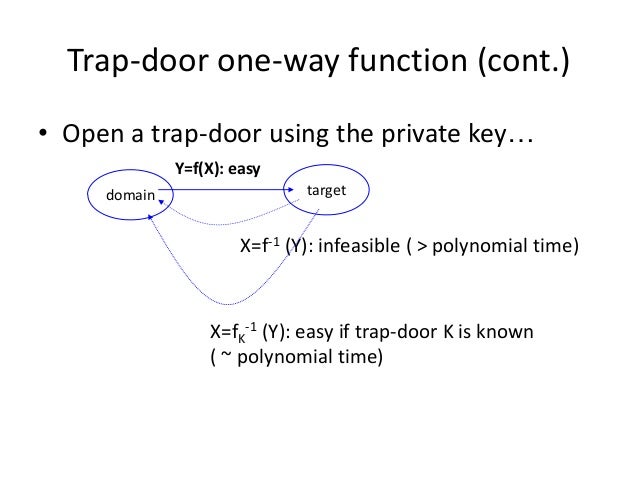
而滿足性質4之單向陷門置換,卻也提供了一種數位簽章的方式,在此情形下加解密函數互為「反函數」。而Trapdoor意味著,只有加上特定之額外訊息,才能將任何經加密函數EBob(‧)之訊息有效解密。以RSA公開金鑰密碼系統而言,Trapdoor訊息就是對模數n因數分解的知識。
公開金鑰密碼系統之架構:
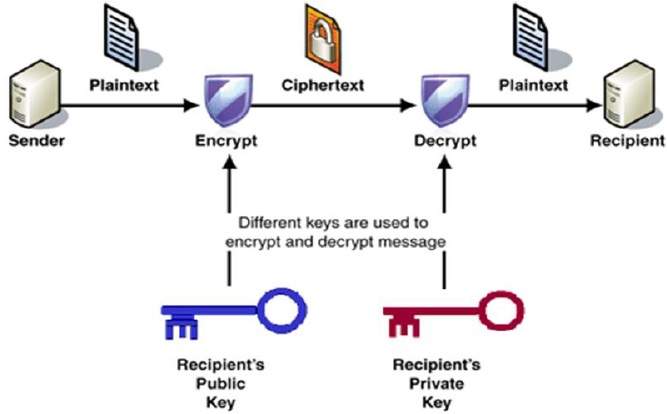
用數學式子來表示該圖的運作程序,假設明文為M、鑰匙配對為{KR, KU}、C為密文。其加密與解密程序為:
加密程序:
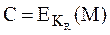
,利用KR加密。解密程序:
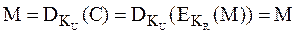
,利用KU解密。
RSA演算法:
RSA的名稱是由Rivest、Shamir與Adleman三人的名字共同組合而成。雖然Diffie與Hellman提出只要能找出單向陷門的函數,便能解決公開金鑰密碼學的問題。但真正提出解決方案的是由Rivest、Shamir與Adleman等三人,也因此定名為「RSA演算法」(RSA Algorithm)。
依據RSA演算法特點,大多運用於密鑰交換與數位簽章兩大方面。其實RSA演算法也可以用來加密與解密功能,達成訊息隱密性傳輸的功能。但它為了提供安全性,金鑰長度都較長,執行加解密時,需耗費較長的時間,因此對於大量資料傳輸並不適合。
利用RSA金鑰加密的特點是,「明文的長度不可以超過金鑰長度」(根據不同補齊方式,能夠加密的長度也不一樣),訊息經由加密編碼後的密文與金鑰長度相同。如果針對大量資料加密的話,則需將明文依照金鑰長度(如1024或2048 bits)分割成若干個區塊,分別加密後再組合成密文序列。解密處理也是相同,分段解密後再組合回原明文格式。
RSA演算法是利用模指數,推演出公開與私有金鑰配對,並能完全合乎單向陷門的需求。RSA演算法同樣使用區塊加密法,且金鑰與區塊明文的長度必須相同。明文區塊被加密成相同長度的密文區塊,每一區塊的數值小於某個整數n,若區塊大小為k個位元,則2^k< n < 2^k+1。對於明文m與密文區塊c來說,其加密與解密函數計算為:
c = E(m) ≡ m^e (mod n)
m = D(c) ≡ c^d
≡(m^e)^d ≡ m^ed(mod n)其中n為加密者與解密者雙方都知道的數值,但加密者必須知道數值e,而只有解密者知道另一個數值d,我們以KU= (n, e)為公開金鑰,以KR= (n, d}為私有金鑰;兩把金鑰可以相互加密或解密。
演算法:
令Alice欲將明文m加密成密文c傳至Bob,而Bob將密文c還原成明文m。
- (金鑰產生)Bob取相異質數p, q(保密),計算RSA模數(RSA Modulus)n=pq並將其公開,取e為加密金鑰將其公開,其中e必須與ψ(n)互質,在此情況 ψ(n) = (p-1)(q-1)(保密)。 Bob之公開金鑰為(n,e);Bob計算d為解密金鑰(保密),(n,d)為Bob之私密金鑰,其中 ed ≡ 1 (mod ψ(n))。
- (加密)Alice取得Bob之公開金鑰(n,e),用加密函數計算 c = E(m) ≡ m^e (mod n),將密文c傳給Bob。
- (解密)Bob用解密函數計算 m = D(c) ≡ c^d (mod n),解密還原成明文。
RSA演算法不同於對稱式密碼演算法如DES、AES、IDEA,公開金鑰(n,e)必須讓欲傳訊者知道,而私密金鑰(n,d)與參數ψ(n)之保密至為關鍵,其中:
RSA演算法可成例之關鍵在於,加解密金鑰e,d滿足 ed ≡ 1 (mod ψ(n)) => 意即在取ψ(n)的模運算下e與d互為乘法反元素,由此可用尤拉定理推導出加密函數E(‧)與解密函數D(‧)互為反函數 => D(E(m)) ≡ m (mod n)且E(D(m)) ≡ m (mod n)。
證明:
由尤拉ψ函數可知 ψ(n) = ψ(p)ψ(q) = (p-1)(q-1),e與d滿足 ed ≡ 1 (mod (p-1)(q-1)),故存在某整數k,使得ed = kψ(n)+1。
考慮 D(E(m)) ≡ (E(m))^d ≡ (m^e)^d = m^ed = m^kψ(n)+1 (mod n)E\(D\(m\)\) ≡ \(D\(m\)\)^e ≡ \(m^d\)^e = m^ed = m^kψ\(n\)+1 \(mod n\)考慮gcd(m,n)值:
若gcd(m,n)=1:由尤拉定理[m^ψ(n) ≡ 1 (mod n)],得m^kψ(n)+1 = (m^ψ(n))^k.m ≡ m (mod n);
若gcd(m,n)=n:m^kψ(n)+1 ≡ 0 ≡ m (mod n);
若gcd(m,n)=p或gcd(m,n)=q:假設gcd(m,n)=p,此時gcd(m,q)=1,由費馬小定理得m^q-1 ≡ 1 (mod q),故m^kψ(n)+1 = m^k(p-1)(q-1)+1 ≡ m (mod q),另一方面,m^kψ(n)+1 ≡ 0 (mod p),所以可由中國餘式定理得m^kψ(n)+1 ≡ m (mod n)。
若ψ(n) = (p-1)(q-1)已知,解密金鑰d可由廣義輾轉相除法計算得知,因此值ψ(n)、p、q要千萬保密。若ψ(n)已知,則p+q=n+1-ψ(n) 可用一元二次方程式解x^2-(n+1-ψ(n))x+n=0。
RSA密碼之關鍵在於p、q為兩大質數時,大整數n之質因數分解為一件極費時的工作,若分解不開n, 則找不到ψ(n)與d,因此就無法從c解得m,在不久以前,要分解一個數的因子仍停留在近乎硬試的階段,即要從2,3,5,7,…,一直試到√n附近才停止。若n是50位數而p、q均近25位數,則分解n要除約1025次,(1980年)若以電腦以每秒10^6次的高速運算,這仍是一個10^11年的工作。[n值一般建議為1024-bit(309位10進位數)]
RSA演算法範例:
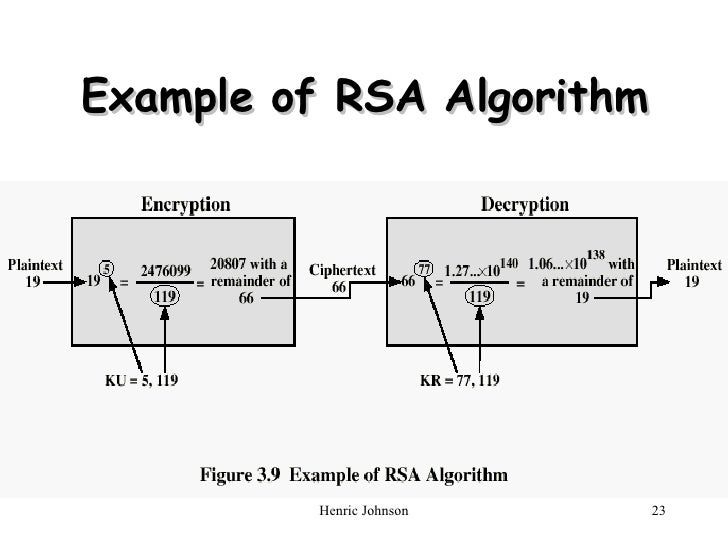
Alice欲將明文m=19加密成密文傳給Bob。
(金鑰產生)Bob選定兩個質數,p = 7、q = 17,
計算n = pq = 7×17 = 119,
在此情況ψ(n) = (p-1)×(q-1) = 6×16 = 96,
選定公開金鑰e,必須滿足gcd(e,ψ(n)) =1,假設取e =5,
Bob之公開金鑰為(n,e)=(119,5),
Bob用廣義輾轉相除法計算解密金鑰d ≡ e^-1 = 5^-1 ≡ 77 (mod 96),其中d <96且必須滿足 de ≡ 1 (mod 96)。
經過上述推演得到:
公開金鑰:KU= {n, e} = {119, 5}
私有金鑰:KR= {n, d} = {119, 77}
(加密)Alice取得Bob之公開金鑰加密得密文 c = m^e (mod n) = 19^5 ≡ 66 (mod 119),則密文為66。
計算過程如下:
19^2 = 361 ≡ 4 (mod 119)
19^4 ≡ 4×4 = 16 ≡ 16 (mod 119)
19^5 = 19^4×19^1 ≡ 16×19 = 304 ≡ 66 (mod 119)
(解密)Bob解密 m = c^d (mod n) = 66^77 ≡ 19 (mod 119),則明文為19。
計算過程如下:
66^2= 72 mod 119
66^4= 72×72 = 5184 = 67 mod 119
66^8= 67×67 = 4489 = 86 mod 119
66^16= 86×86 = 7396 = 18 mod 119
66^32= 18×18 = 324 = 86 mod 119
66^64= 86×86 = 7396 = 18 mod 119
66^77 = 66^64×66^8×66^4×66 = 6845256 = 19 mod 119
RSA安全性:
攻擊RSA演算法有兩種主要的方法:
暴力攻擊法:嘗試所有可能的鑰匙。任何一種密碼演算法都可以被暴力攻擊破解,唯一克服的方法是增加金鑰的長度。
數學攻擊法:既然RSA演算法是利用數論推導出來,所以也一定可以利用數學方法來破解;雖然目前無法百分之一百的成功,但相信新的數學方法被推演出來時,可能致使RSA變得不堪一擊。目前大多採用「因數分解法」來攻擊。
RSA密碼系統本質上為雙質數密碼(Bi-prime Cipher),實作上,必須考量以下兩個質數問:
RSA模數n=pq,其中p、q為兩相異質數,如何找到質數p、q?又如何判斷所找到的數是質數?
RSA模數n是公開的,如果有人能因式分解n=pq,則任何以此模數n之RSA密碼,都可破解,因此模數n不能輕易的被因數分解成了RSA密碼實用上,最最重要的考量了。
在此,我們試圖考量第2個質數問題,即因數分解問題。可由以下簡例中一窺端倪:
Bob之公開金鑰為 (n, e)=(782741, 7)。
攻擊者Eve截收到Alice傳給Bob之密文 144310,並知道他們之間的通訊代碼為:a=0、b=1、.....、z=25。
如果Eve之道n之質因數分解,即之道是何質數p、q使得pq=782741,就可以計算ψ(n) = (p-1)(q-1),再以廣義輾轉相除法計算得解密金鑰d ≡ 7^-1 (mod ψ(n)),便可還原明文代碼 m ≡ 144310^d (mod 782741)。
如何找到質因數p、q,使得pq=782741?
Eve試著從2到小於等於[√782741]=884之質數試除(共計有153個質數),在第150個質數(863)時發現 782741/863=907=q,因此ψ(n)=862*906=780972。
以廣義輾轉相除法得d ≡ 7^-1 ≡ 223135 (mod 780972)。
所以明文代碼為 144310^223135 ≡ 126037 (mod 782741)。
而126037 = 4847*26+15 = (186*26+11)*26+15 = ((7*26+4)*26+11)*26+15 = 7*26^3+4*26^2+11*26+15 = (7,4,11,15),因此明文為 help。
從上例中,可發現在已經有質數表的情況下,Eve還需要計算120次除法,才可分解6位數n=782741,即使是如此小的6位數,質因數分解尚需要如此之多的計算,因此質因數分解一般相信試困難的。
在計算L-bit整數n的因數分解,以目前的演算法來看是困難的,所有的演算法都無法在多項試時間內完成,以「二次篩法」(Quadratic Sieve Method)為例,其計算複雜度為 e^O(√LlnL),而一般的「代數數體篩法」(Algebraic Number Field Method)也須 e^O(L^1/3(lnL)^2/3)。
試著去破解RSA密碼,就意味著,嘗試去質因數分解RSA密碼公開金鑰之RSA模數n。
破解RSA-129是採用某種版本的二次篩法,用以因數分解RSA模數n,二次篩法在解析數論中是一種常見方法,其基本開頭想法是要找出正整數x、y,使得 x^2 ≡ y^2 (mod n)並且滿足 x !≡ +-y (mod n)。
如果n是數x^2-y^2 = (x-y)(x+y)的因數,卻非x-y或x+y的因數,故其gcd(x-y, n)或gcd(x+y, n)均為n之因數,如此便可將n因數分解了。
範例(Fermat因數分解):與二次篩法一樣就是利用式子n^2 = x^2-y^2 = (x+y)(x-y)。
令n=295927。直接計算n^2+1^2、n^2+2^2、....、n^2+k^2,直至n^2+k^2為完全平方數為止。
295927 + 3^2 = 295936 = 544^2,因此可得因數分解 295927 = 544^2-3^2 = (544+3)(544-3) = 547*541。
因有Fermat因數分解 之故,在RSA密碼中質數p、q之選取,一般建議|p-q|不宜太小,故p與q長度宜有數位元之差。
| 年代 | 十進位數之位數 | 備註 | | :---: | :---: | :---: | | 1994 | 129 | RSA-129用二次篩法 | | 1996 | 130 | RSA-130用代數數體篩法 | | 1999 | 155 | RSA-155用代數數體篩法 | | 2003 | 174 | 破譯576-bit RSA | | 2005 | 200 | | | 2009 | 232 | 破譯768-bit RSA |
第一個公開金鑰演算法 Diffie-Hellman金鑰交換(Key Exchange):
回朔到1976年,Diffie-Hellman金鑰交換主要是用在密鑰的產生,而不是用來加密或解密。所碰上的場景為:Alice與Bob在不安全的連線上,共同使用一種對稱式金鑰密碼如DES來加解密,而他們想直接在這連線上,協定出共同所使用之密鑰。
演算法:
Alice與Bob欲協定一共同密鑰。共同取大質數p以及底數g原根 (mod p) (2<= g <=p-2)。
Alice取a∈{0,1,2,....,p-2} 計算 A ≡ g^a (mod p) 將值A傳訊給Bob。
Bob取b∈{0,1,2,....,p-2} 計算 B ≡ g^b (mod p) 將值B傳給Alice。
Alice收到B,計算 K ≡ B^a ≡ (g^b)^a (mod p),K即共同協定之密鑰。
Bob收到A,計算 K ≡ A^b ≡ (g^a)^b (mod p),K即共同協定之密鑰。

即使是不安全的通路傳遞訊息,Eve只知道值p、g、A、B,此時要推算出密鑰K ≡ g^ab (mod p)並非易事,因f(x)=g^x (mod p)為單向陷門函數。若值p、g、A、B已知,欲求密鑰K,如此的問題稱為Diffie-Hellman問題。
此處相關離散對數問題,即解loggA或loggB,只要他能解出任一離散對數問題,他就會知道a或b,可立即計算金鑰K ≡ A^b ≡ B^a (mod p)。
「離散對數函數」為「模指數函數」之反函數,模指數函數計算容易,而離散對數函數計算困難。
離散對數問題(Discrete Logarithm Problem, DLP):
令n、α、β為非零整數,滿足 β ≡ α^x (mod n) (其中n不一定是質數)
尋找解x=logαβ之問題即DLP。
範例:
取(p, g)=(17,3),其中3是原根 (mod 17)。Alice取a=7,計算 A ≡ g^a = 3^7 (mod 17) ≡ 11,
3為17之原根 => 乘法群Z/17^x中之同餘類均可表為[3]之若干次方,
亦即3生成乘法群Z/17^x,即 <3>:={3^i mod 17 | i∈N}=Z/17^x。
並將A=11傳給Bob。Bob取b=4,計算B ≡ g^b ≡ 3^4 (mod 17) ≡ 13,
並將B=13傳給Alice。所以共同協定之密鑰 K = g^ab ≡ 3^7*4 ≡ 3^28 ≡ 4 (mod 17)。
Bob計算 K ≡ A^b = 11^4 ≡ 4 (mod 17);
而Alice計算 K ≡ B^a = 13^7 ≡ 4 (mod 17)。
此金鑰交換演算法在業界廣為使用,在許多安全協定中,如SSL、PKCS#3等都有採用。演算法的安全性建構在DLP,困難度頗高。但在使用時,仍要注意「居中攻擊」(Man in the Middle Attack)的攻擊方法。
居中攻擊(Man in the Middle Attack):
Alice與Bob在極度不安全的通路協定密鑰,當中第三者Eve發動ARP Spoofing,分別扮成Alice與Bob協定密鑰,而Alice與Bob卻渾然不知。Eve藉由以下步驟與Alice、Bob協定密鑰:
Eve選一數c∈{0,1,2,....,p-2},計算 C ≡ g^c (mod p)。
與Alice協定出密鑰 KAlice ≡ g^ac ≡ C^a ≡ A^c (mod p)。
與Bob協定出金鑰 KBob ≡ g^bc ≡ C^b ≡ B^c (mod p)。
如此Eve便可用KAlice與Alice加解密訊息,而與Bob便可用KBob加解密訊息。

由此例可知,當收訊者不能確定訊息給他的人是誰時,其時就存在往安漏洞,而數位簽章(Digital Signature)即可彌補以上漏洞。而Diffie-Hellman金鑰交換只要略為修改,也可適用於多人共用協定密鑰。
範例:
Alice、Bob與Carl欲共同協定金鑰,事先協定使用模數p為質數,底數g為原根 (mod p)。
Alice取值a,計算 A ≡ g^a (mod p),將A傳至Bob。
Bob取值b,計算 B ≡ g^b (mod p),將B傳給Carl。
Carl取值c,計算 C ≡ g^c (mod p),將C傳給Alice。
Alice計算 C' ≡ C^a (mod p),傳值至Bob。
Bob計算 A' ≡ A^b (mod p),傳值至Carl。
Carl計算 B' ≡ B^c (mod p),傳值至Alice。
共同協定之密鑰為 K ≡ g^abc (mod p),而最後計算為:Alice計算 K ≡ B'^a (mod p),Bob計算 K ≡ C'^b (mod p),而Carl計算 K ≡ A'^c (mod p)。