雜湊與訊息驗證

密碼學還有一重要元件，即Hash函數為一固定長度輸出的單向函數。在許多情況中，Hash函數往往是與其他公開金鑰數位簽章演算法配合使用，甚至以此為虛擬亂數產生器。值得一提的是，常使用的Hash函數，如MD4、MD5、RIPEMD都已經找到碰撞，SHA-1的密碼分析，也有重大突破，目前建構於此的資安體系，已經面臨嚴重考驗。

目前Hash函數的主流依然是SHA-1系列以及歐洲所研發之RIPEMD系列，這些都與較早的MD系列類似，乃是採取「壓縮函數」多次迭代作用設計，然而都是因為固定輸出長度，都可以藉由「生日攻擊」將有效安全位元長度減半，甚至也可適用於解離散對數問題。

雜湊函數簡介：

所謂「雜湊函數」(Hash Function)，是將任意長度訊息的輸入，演算成固定長度雜湊值(Hash Value)(又稱為摘要)的輸出，即：

h: {任意長度之訊息} -> {固定長度之摘要(Digest)}

且所計算出來的雜湊值必須符合以下條件：

  1. 給定一訊息m，計算摘要h(m)要非常迅速。
  2. Pre-Image Resistance：給定摘要y，很難找到訊息m使得 h(m)=y。 (此稱h(‧)為單向函數(One-way Function))
  3. Second Pre-Image Resistance：給定訊息m1，很難找到另一個訊息m2(!=m1)使得 h(m1)=h(m2)。 (此處稱為弱抗碰撞(Weakly Collision Resistance))
  4. 很難同時找到不同之m1及m2使得 h(m1)=h(m2)。 (此處稱為強抗碰撞(Strongly Collision Resistance))

雜湊值必須隨明文改變而改變。也就是說，不同明文所計算出來的雜湊值必須是不相同的，甚至僅改變明文中任何一個字元時，雜湊值的輸出也必須差異很大。由此可見，期望中的雜湊值就好像是一個無法冒充的識別碼，且每一份文件都有其特殊的雜湊值，且無法被偽造，故有「數位指紋」(Digital Fingerprint)之稱。雜湊函數在資訊安全技術上所扮演的角色極為重要，應用範圍很廣泛。此章介紹一些標準化的雜湊演算法，也會探討其安全性。

雜湊函數的運算及參數表示如下：

訊息輸入：M

雜湊函數：H

雜湊值輸出： h= H(M)

在實務上，常使用函數為Rivest所研發之MD系列的Hash函數、安全雜湊演算法(SHA)，以及歐洲所研發之RIPEMD-160，其中MD系列多為128-bit，而SHA、RIPE-160為160-bit；但128-bit之雜湊函數都已經找到碰撞，所以128-bit之所有Hash函數都已經不安全。即使是稱之為安全Hash演算法的SHA-1，也面臨考驗。來自中國山東大學的王小云與她的團隊，針對SHA-1等各Hash函數研究，原先要估計2^80次計算才會找到碰撞，根據他們的研究，已經降至2^63。

一般Hash函數內會包括一個重複使用之壓縮函數(Compresion Function)f，該壓縮函數f應有兩輸入即兩變數，一是前次輸入，稱之為串聯變數(Chaining Variable)；另一為文件m之一區塊。經壓縮函數迭代作用後，最後輸出即訊息摘要為n-bit h(m)。其作法為：

  • 將m填補成m'，即L塊b-bit區塊， m' = Y0 || Y1 || Y2 || .... || YL-1。
  • 然後以壓縮函數f迭代作用： c0 = IV = n-bit初始值 ci = f(ci-1,Yi-1) (1<=i<=L) h(m) = cL。
  • 壓縮函數f當然就會成為Hash函數設計的關鍵，以抗碰撞的壓縮函數f所設計之Hash函數，就一定是抗碰撞的。

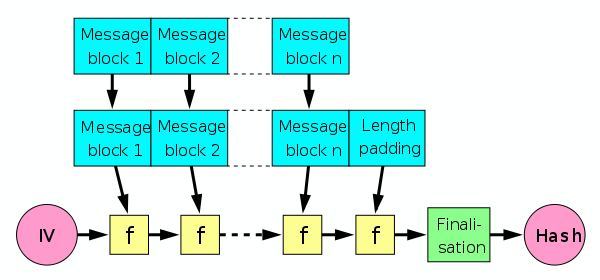Merkle–Damgård hash construction

雜湊函數的簡單應用：

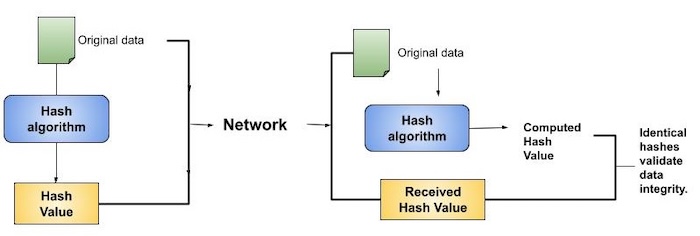
其實在網路通訊方面，雜湊函數常被用來偵測傳輸資料是否有發生錯誤，發送端傳送資料之前，先將資料經過某一種雜湊函數計算，而得到一個雜湊值。然後將這雜湊值附加在資料後面，一併傳送給接收端。接收端收到資料之後，也以相同的雜湊函數計算出另一個雜湊值；如果此雜湊值與傳送端所計算的相同，則表示資料並沒有發生錯誤。一般來講，在較底層的通訊協定(如資料鏈結層)都使用CRC(Cyclic Redundancy Check)除法器，來產生一個檢查資料的FCS(Frame Check Sequence)；至於較高層(如傳輸層)則採用檢查集(Checksum)方法居多。

以checksum為例，不難發現這種雜湊函數的脆弱性。它的運作方式是利用所有字元組成的相對位元之間做XOR(符號為⊕)運算，稱為「位元操作- XOR」(Bitwise-XOR)。首先將訊息以字元(如32、64或128 bits)為一個區塊排列，在區塊之間相對位元做XOR運算。假設將訊息切成m個區塊，每個區塊有n個位元(如32 bits)，則所產生的checksum(或稱雜湊值，也是32 bits)為：

Cj = bj1 ⊕ bj2 ⊕ ,...., ⊕ bjm (j = 1, 2,...., n)。

字元1 B11 B21 B31 ...... Bn1
字元2 B12 B22 B32 ...... Bn2
...... ...... ...... ...... ...... ......
字元m B1m B2m B3m ...... Bnm
雜湊值 C1 C2 C3 ...... Cn

每一雜湊值的位元(Cj)是由該行所有位元做XOR運算而產生，如同同位元(Parity Bit)一般，其中如果有偶數個位元發生錯誤(由1→0、或0→1)，則該位元的雜湊值將不會發生變化，因此，它的偵錯能力是非常薄弱的。

MD5 Hash函數：

「訊息摘要」(Message Digest) MD系列是由Ron Rivest(RSA中的"R")在MIT所發展的一系列雜湊演算法，其中較著名的有MD2(RFC 1319)、MD4(RFC 1320)與MD5(RFC 1321)。MD2主要是以8個位元為單位的計算方式，複雜度較弱，一般都將該演算法崁入於數位晶片上，如IC卡。MD4與MD5都是針對32位元CPU所設計的；MD5是由MD4改良得來，就目前而言，MD5安全性早已在MD4之上。

MD5一開始是將輸入之文件，以每512-bit為一區塊(Block)，而每個區塊再分為16個32-bit之子區塊(Subblock)，將其運算，最後輸出4個32位元之訊息摘要。

MD5演算法架構：

  • MD5是將不定長度的訊息，演算成一個128位元長的訊息摘要(或稱雜湊值)；計算方式是屬於串接式的區塊演算法。

  • 步驟1：將訊息m加上一些附加位元(Padding Bits)，使得訊息長度為448 (mod 512)。若訊息的長度已為448 (mod 512)時，仍需再加入512 bits的附加位元。所附加位元的資料除第一個位元為1，其餘皆為0。

  • 步驟2：加上64 bits長度欄位，其內容表示原訊息的長度，以bit為單位。如果訊息長度K>2^64個位元，則取K (mod 2^64)。

  • 步驟3：以每512 bits為單位，將訊息分割為L個區塊，故 m'=Y[0], Y[1],...., Y[L-1]，其中Y[i] (0<=i<=L-1)為512-bit GF(2)字串。而每一個區塊Y[i]再細分為16個32位元之子區塊，即 X[0], X[1],...., X[15]，其中X[k] (0<=k<=15)為32-bit GF(2)字串。

  • 步驟4：將第一區塊(Y0)與起始向量(Initial Vector, IV，128 bits)輸入到MD5演算法中，輸出為CV1(128 bits)；CV1則作為下一個區塊Y1的輸入，依此類推。

  • 步驟5：最後區塊(YL-1)與前一個CVL-1經由MD5演算後的輸出值，即為該訊息的訊息摘要(或稱雜湊值，128 bits)。起始向量(IV)是一個重要的參數，每次演算時加入不同的IV值，可以增加破解的困難度。一般來說，IV值只要在雙方協商時，以明文傳送即可(亦可加入於原訊息中一起加密)。

MD5演算法：

接下來，我們來探討上圖中的MD5演算法，它有兩組輸入：一組為512 bits的明文區塊(Yq)，另一組為上一區塊所計算出來128 bits的雜湊值(CVq)(第一個區塊為IV值)。經由MD5演算法計算出128 bits的雜湊值(CVq+1)後，繼續傳送給下一個區塊直到結束。

下圖只有一個MD5演算法，分為4個回合計算，每一回合計算16次，而下一個區塊也是不斷重複使用同一個MD5演算法。

每一回合的運算器稱之為「壓縮函數」(Compression Function)，是MD5演算法的核心，它的功能是將512個位元的區塊，攪拌及壓縮成128個位元。

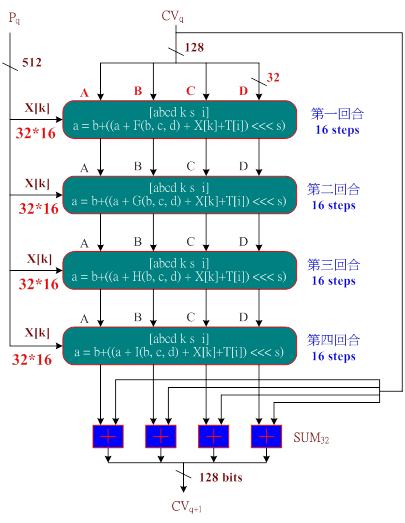一個MD5演算法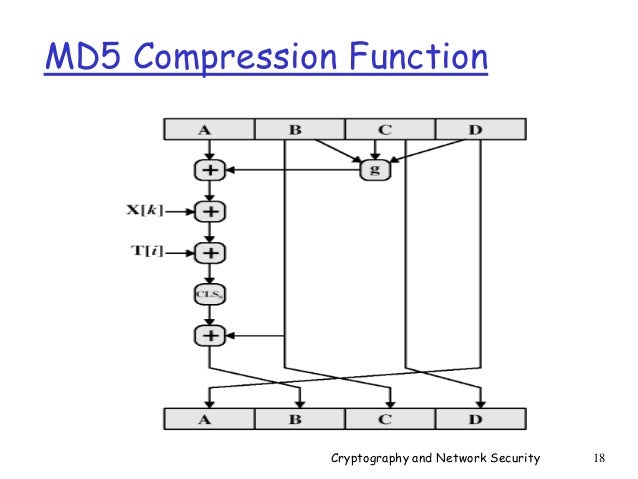MD5 壓縮函數

MD5壓縮函數介紹：

  • (函數暨常數定義)使用4個非線性函數g：
    對MD5而言，四個回合中每回合都有一個非線性函數(F、G、H與I)，並且每一回合都計算16次。

    F(b,c,d) = (b ∧ c) ∨ ((¬b) ∧ d)
    G(b,c,d) = (b ∧ d) ∨ (c ∧ (¬d))
    H(b,c,d) = b ⊕ c ⊕ d
    I(b,c,d) = c ⊕ (b ∨ (¬d))

    其中⊕表XOR、∧表AND、∨表OR、¬表NOT邏輯運算。

  • 定義常數函數T(i)：

    就MD5而言，它使用Sine函數的非線性數值特性，計算方式是T[i] = 2^32×|(sin(i+1)| (i=0,1,....,63)，其中i表示弧度(Radians)；亦即每一次運算取一個T[i]，共64次運算。

  • | T[0] = D76AA478 | T[16] = F61E2562 | T[32] = FFFA3942 | T[48] = F4292244 | | :--- | :--- | :--- | :--- | | T[1] = E8C7B756 | T[17] = C040B340 | T[33] = 8771F681 | T[49] = 432AFF97 | | T[2] = 242070DB | T[18] = 165E5A51 | T[34] = 699D6122 | T[50] = AB9423A7 | | T[3] = C1BDCEEE | T[19] = E9B6C7AA | T[35] = FDE5380C | T[51] = FC93A039 | | T[4] = F57COFAF | T[20] = D62F105D | T[36] = A4BEEA44 | T[52] = 655B59C3 | | T[5] = 4787C62A | T[21] = 02441453 | T[37] = 4BDECFA9 | T[53] = 8F0CCC92 | | T[6] = A8304613 | T[22] = D8A1E681 | T[38] = F6BB4B60 | T[54] = FFEEF47D | | T[7] = FD469501 | T[23] = E7D3FBC8 | T[39] = BEBFBC70 | T[55] = 85845DD1 | | T[8] = 698098D8 | T[24] = 21E1CDE6 | T[40] = 289B7EC6 | T[56] = 6FA87E4F | | T[9] = 8B44F7AF | T[25] = C33707D6 | T[41] = EAA127FA | T[57] = FE2CE6E0 | | T[10] = FFFF5BB1 | T[26] = F4D50D87 | T[42] = D4EF3085 | T[58] = A3014314 | | T[11] = 895CD7B1 | T[27] = 455A14ED | T[43] = 04881D05 | T[59] = 4E0811A1 | | T[12] = 6B901122 | T[28] = A9E3E905 | T[44] = D9D4D039 | T[60] = F7537E82 | | T[13] = FD987193 | T[29] = FCEFA3F8 | T[45] = E6DB99E5 | T[61] = BD3AF235 | | T[14] = A679438B | T[30] = 676F02D9 | T[46] = 1FA27CF8 | T[62] = 2AD7D2BB | | T[15] = 49B40821 | T[31] = 8D2A4C8A | T[47] = C4AC5665 | T[63] = EB86D391 |

  • 定義向左循環位移CLS之數：

    第一回合：s[0,....,15] = [7,12,17,22,7,12,17,22,7,12,17,22,7,12,17,22]

    第二回合：s[16,....31] = [5,9,14,20,5,9,14,20,5,9,14,20,5,9,14,20]

    第三回合：s[32,....,47] = [4,11,16,23,4,11,16,23,4,11,16,23,4,11,16,23]

    第四回合：s[48,....,63] = [6,10,15,21,6,10,15,21,6,10,15,21,6,10,15,21]

  • +：取32位元的同餘加法 (mod 2^32)

運算過程：

  1. 將輸入明文(512 bits)以每32 bits為單位，分別存入16個子區塊X[k]中，其中k =0, 1, 2,...., 15；每一回合的每一次計算分別選入不同的X[k]值。子區塊讀取之順序為： 第一回合： X[0,....,15] = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] 第二回合： X[16,....,31] = [1,6,11,0,5,10,15,4,9,14,3,8,13,2,7,12] 第三回合： X[32,....,47] = [5,8,11,14,1,4,7,10,13,0,3,6,9,12,15,2] 第四回合： X[48,....,63] = [0,7,14,5,12,3,10,1,8,15,6,13,4,11,2,9]
  2. 進入第一回合運算，將A、B、C與D這4個32-bit串聯變數與明文輸入的X[k]，一起輸入到一個「壓縮函數」進行運算。 A、B、C、D之初始值為： A = 0x01234567 B = 0x89abcdef C = 0xfedcba98 D = 0x76543210

  3. 每次處理的壓縮函數的輸入參數為[abcd, k, s, i]，其中abcd表示上一次執行的四個串聯變數、k表示輸入明文的區段X[k]、i表示sine函數的參考值T[i]、s表示向左迴旋的次數。輸出時，bcd三個串聯變數的內容不變，但a修改成a = b+((a+F(b, c,d)+X[k]+T[i]) <<<s)。本回合需連續執行16次，各次的輸入參數如下：

    | [ABCD, 0 7 1] | [DABC, 1, 12, 2] | [CDAB, 2, 17, 3] | [BCDA, 3, 22, 4] | | :--- | :--- | :--- | :--- | | [ABCD, 4, 7, 5] | [DABC, 5, 12, 6] | [CDAB, 6, 17, 7] | [BCDA, 7, 22, 8] | | [ABCD, 8, 7, 9] | [DABC, 9, 12, 10] | [CDAB, 10, 17, 11] | [BCDA, 11, 22, 12] | | [ABCD, 12, 7, 13] | [DABC, 13, 12, 14] | [CDAB, 14, 17, 15] | [BCDA, 15, 22, 16] |

    以第二次執行為例，其輸入參數為[DABC, 1, 12, 2] (k=1, s =12, i=2)，表示先計算a = b+((a+ F(b, c, d)+ X[1] + T[12]) <<< s[2])，再將上一次運算的D、A、B、C串聯變數分別填入本次的A、B、C與D串聯變數中，然而B、C與D串聯變數的內容不變。

  4. 進入第二回合運算。同樣執行16次，但變更a的函數為G，則a = b+((a+G(b, c, d)+X[k]+T[i]) <<<s[j])；每次輸入的參數如下：

    | [ABCD, 1,5, 17] | [DABC, 6, 9, 18] | [CDAB, 11, 14, 19] | [BCDA, 0, 20, 20] | | :--- | :--- | :--- | :--- | | [ABCD, 5, 5, 21] | [DABC, 10, 9, 22] | [CDAB, 15, 14, 23] | [BCDA, 4, 20, 24] | | [ABCD, 9, 5, 25] | [DABC, 14, 9, 26] | [CDAB, 3, 14, 27] | [BCDA, 8, 20, 28] | | [ABCD, 13, 5, 29] | [DABC, 2, 9, 30] | [CDAB, 7, 14, 31] | [BCDA, 12, 20, 32] |

  5. 進入第三回合運算。同樣執行16次，改變a的函數為H，則a = b+ ((a+ H(b, c, d)+ X[k]+T[i]) <<<s[j])；每次輸入的參數如下：

    | [ABCD, 5, 4, 33] | [DABC, 8, 11, 34] | [CDAB, 11, 16, 35] | [BCDA, 14, 23, 36] | | :--- | :--- | :--- | :--- | | [ABCD, 1, 4, 37] | [DABC, 4, 11, 38] | [CDAB, 7, 16, 39] | [BCDA, 10, 23, 40] | | [ABCD, 13, 4, 41] | [DABC, 0, 11, 42] | [CDAB, 3, 16, 43] | [BCDA, 6, 23, 44] | | [ABCD, 9, 4, 45] | [DABC, 12, 11, 46] | [CDAB, 15, 16, 47] | [BCDA, 2, 23, 48] |

  6. 進入第四回合運算。同樣執行16次，改變a的函數為I，則a = b+ ((a+ H(b, c, d)+ X[k]+T[i]) <<<s[j])；每次輸入的參數如下：

    | [ABCD, 0, 6, 49] | [DABC, 7, 10, 50] | [CDAB, 14, 15, 51] | [BCDA, 5, 21, 52] | | :--- | :--- | :--- | :--- | | [ABCD, 12, 6, 53] | [DABC, 3, 10, 54] | [CDAB, 10, 15, 55] | [BCDA, 1, 21, 56] | | [ABCD, 8, 6, 57] | [DABC, 15, 10, 58] | [CDAB, 6, 15, 59] | [BCDA, 13, 21, 60] | | [ABCD, 4, 6, 61] | [DABC, 11, 10, 62] | [CDAB, 2, 15, 63] | [BCDA, 9, 21, 64] |

  7. 輸出訊息摘要。將第四回合最後一次的運算結果，與原來輸入區段(CVq)的相對應串聯變數(A、B、C與D)相加後，得到本區段的輸出(CVq+1)，兩個串聯變數(32 bits)相加時，採取 (mod 2^32)。

SHA系列 Hash函數：

美國NIST，在制訂DSA之後，於1993年制定了DSS之Hash函數標準，即「安全雜湊演算法」(Secure Hash Algorithm, SHA)。SHA主要架構承襲了MD系列的函數，其設計方式與MD5非常相似，有所不同的是，MD系列之Hash摘要大都是128-bit，而SHA之訊息摘要為160-bit。就其安全性而言，當然以SHA較為良好。稍後於1995年推出了修訂版，即SHA-1，首先列出SHA-1的特性，再來推演它的演算法，特性如下：

  • 可以輸入任意長度的訊息，訊息經過附加位元後長度須為448 (mod 512)。填補方式與MD5一樣，需加入64位元的長度欄位。

  • 附加位元後的訊息，以512位元為單位，分割成若干個區塊；雖然，區塊的長度為512個位元；但每一區塊再細分成16個32位元的子區塊，之後再經過擴充字元，填入32位元的W[t]，總共有80個(t =0, 1, 2, , 79)。

  • 每個步驟計算與最後運算的結果，皆得到160個位元的雜湊值。

  • SHA-1區塊之間的演算法架構和MD5一樣。

  • 利用5個32位元的串聯變數(A、B、C、D與E)，演算中的160位元的雜湊值。

  • 演算法步驟共有4個回合，每回合執行20次，共計80次的運算。

  • 每回合含一個非線性函數，總計有4個函數(f1、f2、f3、f4)；並於每回合加入一個固定常數(K1~K4)。

  • SHA-1演算法亦是屬於區塊運算方式，但較特殊的地方，是將512個位元區塊擴充成80個32個位元的子區塊，每個執行步驟輸入一個小區塊。

SHA-1演算法：

左圖只有一個SHA-1演算法，分為4個回合計算，每一回合計算20次，而下一個區塊也是不斷重複使用同一個SHA-1演算法。

右圖為每一回合的運算器稱之為「壓縮函數」(Compression Function)，是SHA-1演算法的核心，它的功能是將512個位元的區塊，攪拌及壓縮成160個位元。

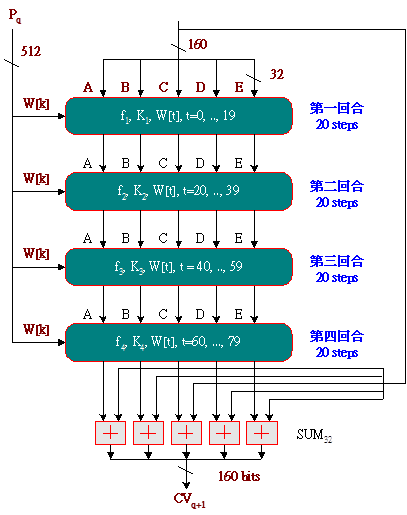
SHA-1壓縮函數介紹：

  • (函數以及常數的定義)SHA-1在四回合中所用之非線性函數分別為f[i] (i=0,1,....,79)定義為：
    第一回合f1：f[i](b,c,d) = (b ∧ c) ∨ ((¬b) ∧ d)，若 0<=i<=19
    第二回合f2：f[i](b,c,d) = b ⊕ c ⊕ d，若 20<=i<=39
    第三回合f3：f[i](b,c,d) = (b ∧ c) ∨ (b ∧ d) ∨ (c ∧ d)，若 40<=i<=59
    第四回合f4：f[i](b,c,d) = b ⊕ c ⊕ d，若 60<=i<=79

  • 定義4個常數為：
    第一回合K1：K[i] = 0x5a827999, 0<=i<=19
    第二回合K2：K[i] = 0x6edgebal, 20<=i<=39
    第三回合K3：K[i] = 0x8f1bbcdc, 40<=i<=59
    第四回合K4：K[i] = 0xca62c1d6, 60<=i<=79
    其實這些常數是分別來自於2^30*√2、2^30*√3、2^30*√5、2^30*√10

  • +：取32位元的同餘加法 (mod 2^32)。

  • <<< s：表示左旋s位元。

  • 另外5個串聯變數之初始值(MD5用4個)分別為：

    A = 0x67452301

    B = 0xefcdab89

    C = 0x98badcfe

    D = 0x10325476

    E = 0xc3d2e1f0

  • 訊息擴充W[t]：將訊息(512個位元)擴充成80個32位元的子區塊(W[t], t=0, 1, …, 79)。其方法是，首先將訊息以每32位元為單位，分割為16個小區塊，分別存入W[0]、W[1]、…、W[15]之中，而第16個以後的小區塊，分別以下面公式計算填入：

    W[t] = S1(W[t-16] ⊕ W[t-14] ⊕ W[t-8] ⊕ W[t-3]) ,t =16, 17, …, 79

    例如：W[16] = S1(W[0] ⊕ W[2] ⊕ W[8] ⊕ W[13])

    其中S1表示向左迴旋一個位元的意思。由此可見，SHA-1的訊息擴充方法是，前面16個子區塊是由原訊息分割得來；而第16個子區塊以後，是由前面某4個子區塊執行XOR運算之後，再向左迴旋一個位元。如此說來，應該可以完全攪碎訊息的關聯性。

破解雜湊函數：

基本上，雜湊函數是將原來訊息打亂，得到另一個唯一亂無章法的雜湊值，而且是越亂越好。很不幸的，我們發現大部分的傳輸訊息都有一定的格式，譬如，信件一開始就有"Dear"，結束時又出現"Your Best Regards"。或者資料檔案都有一定的格式，攻擊者如果知道了明文，就可以依照這些標準格式去修改內容，以達到相同的雜湊值。

我們用一個例子來說明，假設Alice希望約Bob明天見面(See you tomorrow)，寫好了信件，並建立了雜湊值(也許經過加密)，她想應該很安全就交由Eve去發送；Eve原來就愛慕著春嬌，看了這封信當然很不高興，就利用他的資訊安全專長，找出(See you yesterday)、(See you upset)、(don’t see you again)等等，只要能符合相同的雜湊值即可，再將偽造信與Alice簽署的簽署碼(加密的雜湊值)一起發送給志明，如此一來，就達到破壞他們之間的感情目的。

生日攻擊法：Hash函數的攻擊方式，最常用的就是所謂的生日攻擊(Birthday Attack)，而實質上就是利用「機率」性質進行隨機攻擊，首先先就「生日問題」(Birthday Problem）的特性來觀察。

生日問題：當同一房間內有23人，相同生日之機率>50%，若有30人，則相同生日機率>70%。

為何？純粹機率問題。假設有r個同訊息m1,m2,....,mr，而在Hash函數h(‧)作用下，有固定長度l-bit，故所有摘要的可能性共有n=2^l個。r個訊息經Hash函數h(‧)對應到n個不同摘要的可能性，共有n^r個。而每個摘要最多只有一個訊息mi對應到之可能性，共有n(n-1)....(n-(r-1))個；所以，所有出現相同摘要之對應方式共有n^r-n(n-1)....(n-(r-1))個，故其機率為p=n^r-n(n-1)....(n-(r-1))/n^r。
故令λ=r^2/2n，所以有相同摘要之機率為p≈1-e^-λ。

例；某Hash函數h(‧)之摘要為60-bit，故其所有摘要之總數為n=2^60，Eve想要攻擊之，並事先找出35處可能些微改變，並將其一共2^35之摘要儲存，此時它只要比較其摘要，就大約可能攻擊成功。r=2^35, n=2^60代入得λ=512，故其攻擊稱公之機率為p≈1-e^-512≈1。

破解SHA-1函數：

Google 的研究人員創造了電腦加密學在 2017 年的第一個里程碑：攻破了SHA-1安全加密演算法。

這次攻破被命名為 SHAttered attack。研究者提供兩張內容截然不同、色彩明顯差異，但 SHA-1 值卻完全相同的 PDF 檔案為證明：

本次 Google 對其進行攻破花費巨額的演算法：總計 9,223,372,036,854,775,808──超過 9 兆次演算。

破解分為兩階段，分別需要一個 CPU 進行 6,500 年，和一個 GPU 進行 110 年的計算才可完成。這是因為研究者採用自行研發的 Shattered 破解方法，其效率遠勝於暴力破解。且 Google 雲端平台提供的大規模計算技術，明顯減輕了負擔。

但至少目前，人們並不需要恐慌。首先就事件本身而言，普通網友不需要擔心有人會用它做壞事，因為 Google 漏洞披露政策規定，本次 SHAttered attack 的研究者需要等待 90 天才能釋出原始程式碼。就算掌握了程式碼，至少也得有 Google 這種水準的大規模演算能力。

Google 早在 2014 年就未雨綢繆，發表逐步放棄 SHA-1 的決定。前年開始，Google 的 Chrome 瀏覽器已經不再支援 SHA-1 證書，會將其記號為不安全。當證書過期後，瀏覽器將無法存取這些網站。Google 方面也建議 IT 人士採用 SHA-256 等更安全的算法。所以今天的實驗結果宣布，也算是給 SHA-1 補上遲來的一刀。

訊息驗證(Message Authentication)：

當Bob由網路收到一份由Alice傳來的訊息時，Bob首先考慮到的問題是：

  1. 該訊息在傳遞當中是否遭受他人竄改？

  2. 該訊息真的是由Alice所發送或是其他人冒名發送的？

解決上述第一個問題，需仰賴「完整性檢查」(Integrity Check)即可。至於要完全解決第一與第二個問題，則需要良好的「訊息驗證」(Message Authentication)機制不可。換言之，欲保障所收到的訊息無誤的話，可區分為完整性檢查與訊息驗證等兩個層次。基本上，「訊息驗證」與「數位簽章」(Digital Signature)，都是被設計來解決上述兩大問題的技術。且兩者都需要使用金鑰來表明身分，不過對金鑰的來源，之間有很大的差異。

一般來講，「訊息驗證」是以雙方共享的秘密金鑰來確認傳送者的身份；「數位簽章」大多是以傳送者的公開金鑰來確定身份。至於兩者的應用範圍也有很大的區隔，一般「訊息驗證」較著重於訊息傳輸方面；「數位簽章」則大多使用於身份識別方面（如PKI架構），本章以訊息驗證為主要介紹對象。

完整性檢查值(Integrity Check Value, ICV)：

所謂「完整性檢查值」是利用雜湊函數（如MD4、MD5、SHA-1）而得。通常傳送端發送訊息之前，會先將訊息經過某一個雜湊函數計算出雜湊值，再將此雜湊值附加在訊息的後面，一併傳送給接收端；接收端收到訊息之後，也以相同的雜湊函數計算出雜湊碼，如果所計算出的結果與訊息後面的雜湊值相同的話，即表示訊息在傳輸當中未遭受它人竄改。由於此雜湊值為檢查訊息是否遭受竄改的依據，因此稱為「完整性檢查值」。

基本上，完整性檢查不會使用到金鑰，並沒有利用到加密/解密機制，其安全性完全仰賴雜湊函數的強度而定。但就安全性通訊而言，強度再強的雜湊演算法都不能保證其絕對可靠性，因此，完整性檢查值大多在有保護的安全連線下傳輸。為配合各種安全連線的傳輸，ICV可分下列兩種製作方式：

  1. 由明文計算ICV： 表示利用某一種雜湊函數直接將明文M計算出一個ICV值，再將ICV附加在訊息後面傳送給對方；接收端也將所收到的訊息M'經過同一種雜湊函數計算出另一個ICV值，如果兩個ICV值相同的話，則表示訊息是正確的。在此機制下，ICV值與訊息都是以明文傳送，並沒有任何安全考量；攻擊者取得訊息之後，可試著竄改訊息內容以得到相同的ICV值，如此一來，便可達到攻擊的目的。由此可見，由明文計算ICV機制僅適合於有安全保護下的連線使用；不然就得將訊息與ICV值一起加密後，再傳送給對方。
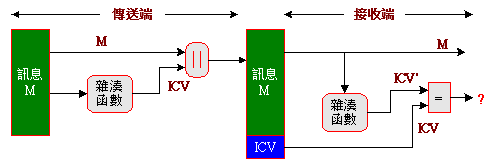
  2. 由密文計算ICV： 表示訊息經過加密之後，再利用密文來計算ICV值，並將ICV值與密文一起傳送給接收端。很明顯可看出，它的安全性會比明文計算高一點，攻擊者若想藉由修飾沒有規律的密文，產生相同的ICV值，似乎不是那麼容易，因此可以獨立作業，不一定非得在有安全保護的連線下傳輸。一般對比較不重要的訊息，利用此機制來傳輸即可(反正訊息已加密)，不需要額外的安全連線。

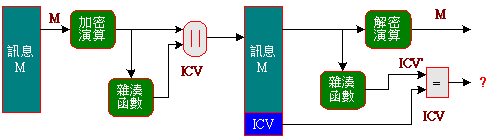
訊息鑑別碼(Message Authentication Code, MAC)：

是經過特定演算法後產生的一小段資訊，檢查某訊息的「完整性」以及「身分驗證」。它可以用來檢查在訊息傳遞過程中，其內容是否被更改過，不管更改的原因是來自意外或是蓄意攻擊。同時可以作為訊息來源的身分驗證，確認訊息的來源。

MAC的演算法，常用的方法，就是會使用任一區塊密碼演算法，以CBC模式加密，只保留最後一個區塊所產生之密文當作MAC。

CBC-MAC 演算法：

輸入：訊息m，特定區塊密碼演算法E以及密鑰K。

輸出：n-bit m之MAC h，(n為E之區塊位元長度)。

  1. 將訊息m分割成以n-bit大小為單位之區塊，並將最後一個區塊填補資料 m = m1 || m2 || ... || mx。
  2. (CBC模式加密)令Ek為密鑰K之加密函數，計算： h1 = Ek(m1) hj = Ek(hj-1 ⊕ mj)， (j=2,3,....,x) 只需保留hx值，其餘hj(j=1,2,....,x-1)皆無須保留。

若所採用之區塊密碼演算法為DES，則稱為「DES-MAC」演算法。這種演算法已被FIPS發表為標準(FIPS PUB 113)，同時也成為ANSI的標準(X9.17)，所產生的鑑別碼稱為「資料鑑別碼」（Data Authentication Code, DAC）。

DES-MAC使用DES的CBC模式，並將起始向量設定為零。DES-MAC的運作如下：

  1. 首先將欲確認的資料以64個位元為單位，分割成若干個區塊(D1, D2,...., DN)，其中如有不足的部分全部補上0
  2. 接下來，以區塊為單位，連續送給DES演算法運算，計算時會輸入56位元的加密金鑰(或稱秘密金鑰)，輸出的密文仍為64個位元。前一區塊所產生的密文，與本次的區塊明文之間執行XOR運算，再進入DES演算法；依此類推，直到最後區塊的密文輸出(64 bits)。由最後輸出的密文(ON)中取最高位元的若干位元(16 ~ 64 bits)，作為MAC值(或稱DAC)的輸出。

雖然DES-MAC是採用56位元金鑰的DES演算法，但許多地方為了提高安全性，也漸漸採用128位元的AES演算法。

HMAC(Hash-based Message Authentication Code)：

另外，MAC也不一定要借助於區塊加密演算法實踐，其實也可以用常用之Hash函數，如MD5、SHA-1或是RIPEMD完成，同時結合一個加密金鑰，此即以雜湊為基礎之MAC(Hash-based Message Authentication Code, HMAC)，它可以用來保證資料的完整性，同時可以用來作某個訊息的身分驗證。

根據RFC 2104，HMAC的公式為：

其中：

  • H 為密碼雜湊函式(如MD5或SHA-1)

  • K 為密鑰(secret key)

  • m 是要認證的訊息

  • K' 是從原始金鑰K匯出的另一個秘密金鑰(如果K短於雜湊函式的輸入塊大小，則向右填充(Padding)零；如果比該塊大小更長，則對K進行雜湊)

  • || 代表串接

  • opad 是外部填充(0x5c5c5c…5c5c，一段十六進位常數)

  • ipad 是內部填充(0x363636…3636，一段十六進位常數)

下圖為HMAC產生過程：

results matching ""

    No results matching ""