對稱式金鑰密碼系統

所有的傳統加密演算法都是對稱式金鑰(秘密金鑰)加密法，在 1970年代的公開金鑰加密法發明之前，這是唯一的加密方式。使用對稱式金鑰加密時，只有經過授權並擁有相同金鑰的人，才可以讀取資訊的內容。

對稱式金鑰加密的優點：速度相當快，而且很容易利用軟體或硬體複建置秘密金鑰。

對稱式金鑰加密的缺點：無法確認建立金鑰、加密和傳送有效訊息的人。(相關的人可能有此秘密金鑰)

一般而言，對稱式加密分為2種運算方式：

  • 串流加密 (Stream Cipher) ：對明文一個位元一個位元地加密，就好像是明文不斷的流動進入加密器中加密，加密快速，因此能夠做到及時(real time response)的效果，適合用在語音傳輸加密中，例如VoIP。特色如下：

    • 在加解密時，一次處理一個位元(bit)或位元組(byte) 。

    • 串流加密法適用於通訊上，因為其電路設計較區塊加密法簡單，加密速度比區塊加密法快很多。

  • 區塊加密 (Block Cipher)：把明文切成固定大小的區塊，並用相同的密碼演算法和密鑰對每組分別進行加密和解密。由於要收集一定的資料量才可以做加密的動作，因此比較適合用來做檔案的加密，例如電子郵件加密或銀行交易轉帳。

區塊加密基本原理：

  • 數位資料是一串不定長度的0與1組合而成，對於它的密碼系統就很難直接用取代與移位方法，而需要資料分段來加密或解密，這就是「區塊加密法」(Block Cipher)。它將不定長度的資料，以某一固定長度為單位(大多是64 bits)，分割為若干個區塊。每一明文區塊經過加密編碼後，產生相同長度的密文區塊。

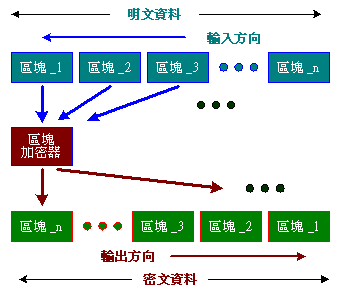
    一個明文資料M被分割成許多小區塊後，表示為：M1 || M2 || M3 ||.....|| Mn，每個區塊都使用相同的金鑰(key)來加密，最後可得到密文：C = Ek(M) = Ek(M1) || Ek(M2) || Ek(M3) ||.....|| Ek(Mn)。既然，我們將明文區分為若干個區塊，來產生同等量的密文。區塊加密法就是探討如何將這固定長度的明文，加密成相同長度的密文。

  • 許多對稱式區塊加密法都是以「Feistel Cipher」的結構為基礎。其想法源自於對「有效地解密」的需求，也就是讓一個明文區塊產生唯一的密文區塊，讓加解密程序為可逆(reversible)。

  • 區塊加密可視為極大量的取代加密法 • 對 64 位元的區塊加密來說，需要 2^64 個項目的表格以用來對應加解密的想法，其原理來自於前面介紹的取代及移位的混合式(mixed)加密法。

區塊密碼加密模式：

區塊加密法是連續的將明文區塊一個接一個加密成密文區塊。基本上，每一明文區塊各對應著一個密文區塊，如果沒有經過特殊處理的話，破解者可以比對明文與密文區塊配對，則可容易地找出加密金鑰。為了增加密文破解的困難度，我們將連續產生的密文區塊之間做特殊處理，如此一來，破解者就無法找出明文與密文區塊配對，增加破解的困難度。以任一特定加密演算法，都可以使用不同的模式做加密的動作，一般而言，可以區分為四種加密模式：

  1. 電子密碼簿 (Electronic Code Book, ECB)
  2. 密碼區塊串聯 (Cipher Block Chaining, CBC)
  3. 密文回饋 (Ciphertext Feedback, CFB)
  4. 輸出回饋 (Output Feedback, OFB)

電子密碼簿模式 ECB：

  • 最自然、最簡單的加密操作模式。它的做法是將訊息P分割成等大小的區塊，即P = P1 || P2 || P3 || .... || PN，當中最後一個區塊要補足一區塊單位的資料，然後分別以固定的加密金鑰(K)下之加密函數E加密，即C = C1 || C2 || .... || CN。

  • 加密方式：
    明文：P = P1 || P2 || P3 || .... || PN
    密文：C = EK(P) = EK(P1) || EK(P2) || EK(P3) || .... || EK(PN)

  • 解密方式：
    密文：C = C1 || C2 || C3 || .... || CN
    明文：P = DK(C) = DK(C1) || DK(C2) || DK(C3) || .... || DK(CN)

  • ECB之優點：因各區塊之運算可獨立運作，即使在部分區塊傳輸運算上發生錯誤，也不會影響到其他區塊，加解密都可平行處理運算。

  • ECB之缺點：若文件中多次重複的明文，又符合區塊大小，可能會產生相同密文，這對於統計式攻擊相當不利，不適合長文件之加密處理。

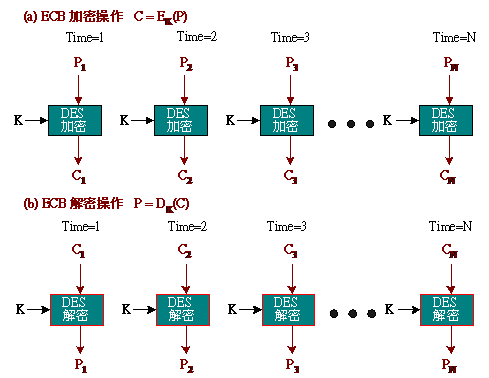    ECB模式DES演算法

密碼區塊串聯模式 CBC：

  • ECB模式最大缺點是可以比對出明文與密文區塊之間的關係，藉此找出加密金鑰，CBC模式就是為了彌補這個缺憾而設計的。

  • 相同的明文區塊並不會產生同樣的密文區塊。

  • 適用於大量訊息加密。

  • 實際做法如下：

    1. 先選取雙方同意之一區塊大小之資料IV，即初始向量(Initial Vector)，該向量可公開之。

    2. 第一輪時(Time = 1)，P1與起始向量(IV)作XOR運算，然後再將運算後的結果導入加密器(或演算法)處理，而得到第一個區段的密文C1。

    3. 第二輪時(Time=2)，將上一次的加密區塊C1與本次的明文區塊做XOR運算，然後再將其結果導入加密器作處理，而得到本輪的密文區塊C2。

    4. 依此類推，先將上一次的密文與本次的明文區塊做XOR運作後，再進入加密器編碼，如此便稱為「密碼區塊串聯」。每一密文區塊的輸出除了與本身明文有關之外，又加上一次的密文來產生本次的密文區塊，因此無法比對出每一區塊明文與密文之間的關係。

    5. 而解密的處理程序只要將加密的運作程序轉換過來即可。

  • 加密方式：

    C1= EK(IV ⊕ P1)

    Ci= EK(Ci-1 ⊕ Pi) (i = 2, 3, 4,...., N)

    C = C1 || C2 || C3 || .... || CN

  • 解密方式：

    P1= DK(C1) ⊕ IV

    Pi= DK(Ci) ⊕ Ci-1 (i = 2, 3, 4,...., N)

    P = P1|| P2 || P3 || .... || PN

  • 驗證：

    DK(Ci) = DK( EK(Ci-1 ⊕ Pi)) (i = 2, 3, 4,...., N)

    = (Ci-1 ⊕ Pi)

    所以DK(Ci) ⊕ Ci-1 = (Ci-1 ⊕ Pi) ⊕ Ci-1 = Pi得證之。

  • CBC之優點：一般而言，使用不同的IV對相同的明文，用CBC模式加密應會得到不同密文。但由於加密之計算與前次區塊有關，所以明文區塊之順序改變或整塊密文區塊被替換，解密便不可能，可以防止他人蓄意攻擊。

  • CBC之缺點：某區塊傳輸錯誤，會影響後面區塊資料傳輸，而且會影響後一個區塊的計算。

  • 與ECB不同之處，就是CBC加密時無法用平行處理的方式，但解密時，由於在做XOR之前就已經知道Ci及Ci-1，所以式可以做平行處理的。

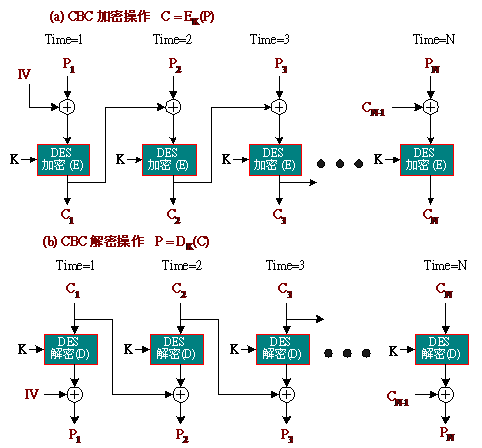    CBC模式DES演算法

密文回饋模式 CFB：

  • 前面兩種加密模式(ECB與CBC)都是屬於區塊加密(Block Cipher)方式，每次輸入加密器(或DES演算法)的資料都是以64個位元為單位，若輸入訊息不足，則必須將原來訊息補足為64位元。但有許多應用系統並不適合區塊加密方式，而是希望每次以少量，並且是連續性的加密。最明顯的應用是交談式的電腦通訊，雙方每次以交談式傳送少量資料給對方，同時希望對方能即時(Real-time)回應。

  • CFB模式加解密只用到加密函數E，未用到解密函數，因此無法適用時公開金鑰密碼系統，只能適用對稱式金鑰密碼系統。

  • CFB加密模式就是將DES區塊(64個位元區塊)加密的方式，轉換成「串流加密」(Stream Cipher)。

  • CFB加密模式每次處理J個位元的加密，加密後的密文也是J個位元，並將加密的結果串接到下一回合的加密輸入，一般應用上都是採用8個位元(J = 8)的加密，這是因為一般資料的編碼都是以8個位元方式(如ASCII碼)。但為了不去修改原來DES演算法，加密與解密的運算還是以64個位元為單位。

  • 實際做法如下：

    1. 首先將訊息以每J個位元為單位(Pm, m = 1, 2,...., N)，一個單位接一個單位連續著進入加密器內處理，每一單位的密文也是J個位元(Cm, m = 1, 2,...., N)，並以串流方式輸出，且前一回合的密文輸出被導入到下一回合的演算法輸入。

    2. 第一回合為第一筆資料輸入加密器(或演算法)，此時「起始向量」(IV, 64 bits)已被事先填入「移位暫存器」(Shift Register, SR, 64 bits)內。

    3. 將移位暫存器的內容輸入到DES加密器內，以秘密鑰匙(K)來加密處理，DES輸出同樣也是64 bits(EK(SR))。接下來，擷取DES加密器輸出的最高J個位元(一般都取8個位元)，與明文資料Pm (m = 1, 2, …, n, J個位元)的每一相對位元之間作XOR運算處理，經運算後輸出便是密文Cm (m= 1, 2, …, n, J個位元)，而DES加密輸出較低位元的部分(64-J個位元)便被捨棄掉了。

    4. 當下一筆資料(Pm+1)再進入時，加密器也進入下一回合的處理。首先將移位暫存器的內容(原IV值)向左移位J個位元(8個位元)，捨棄較高位元部分，而移位時較低位元則由上一回合的輸出(Cm, J個位元)補上，接下來回到步驟2。

  • 在實用上，傳訊中的錯誤對CFB之影響，會隨者暫存器值變化的情況，影響後面連續8個小單位密文的解密。

    假如C1發生錯誤，變成C1'，暫存器值的變化如下：

    SR2 = ******* || C1'

    SR3 = ****** || C1' || C2

    ........

    SR9 = C1' || C2 || C3 || .... || C8

    SR10 = C2 || C3 || C4 || .... || C9

    暫存器SR10之後又恢復正確，也就是說P10, P11, ....又回復正確值。

  • 加密方式： (Sj表示向左移位J個位元、Fj表示選擇較高J個位元、Pm與Cm皆為J個位元、SR為移位暫存器)

    SR1= IV

    C1= Fj(EK(SR1)) ⊕ P1

    SRm= Sj(SRm-1) || Cm-1 (m = 2, 3, 4,...., N)

    Cm= Fj(EK(SRm)) ⊕ Pm (m = 2, 3, 4,...., N)

    C = C1 || C2 || C3 || .... || CN

  • 解密方式：

    SR1= IV

    P1= Fj(DK(SR1)) ⊕ C1

    SRm= Sj(SRm-1) || Cm-1 (m = 2, 3, 4,...., N)

    Pm= Fj(DK(SRm)) ⊕ Cm (m = 2, 3, 4, …, N)

    P = P1 || P2 || P3 || .... || PN

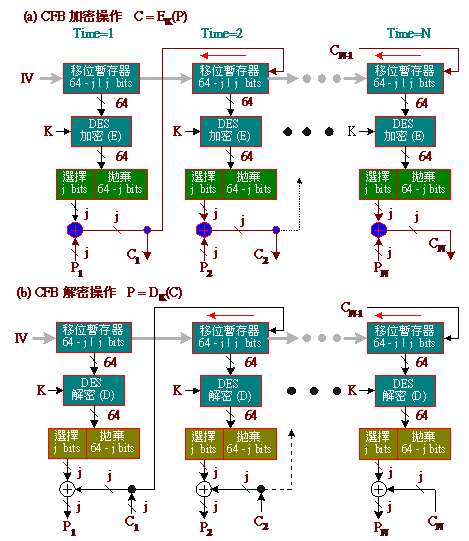    CFB模式DES演算法

輸出回饋 OFB：

  • OCB模式與CFB非常相似，都是屬於串流加密方式，也適用於即時性的交談式連線，譬如，安全性的Telnet連線。並且與CFB一樣不適用於公開金鑰密碼系統，只能用於對稱式今鑰密碼系統。

  • 但CFB模式的密文是經由明文與DES加密輸出之間做XOR運算後的結果，這裡有一個先天性的缺點，就是如果上一筆資料發生錯誤將導致之後密文產生連續性的錯誤。交談式連線有一個特點是，連線的時間較長，而每次傳輸的資料較短，因此在長時間的通訊下，並不能保證傳輸中的資料不會發生錯誤。若採用CFB操作方式，只要有一筆資料發生錯誤，就可能會導致通訊連線中斷

  • 因此OFB模式就是針對CFB這方面的缺點來改善，OFB模式的反饋數值與輸入資料無關，如此可避開錯誤資料的連鎖反應。但因為OFB模式的密文與明文之間對應關係，比較容易遭受明文攻擊(如ECB模式)，這是它主要的缺點。

  • 加密方式： (Sj表示移位J個位元、Fj表示選擇較高J個位元、Pm與Cm皆為J個位元、SR為移位暫存器)

    SR1= IV

    O1= Fj(EK(SR1))

    C1= P1 ⊕ O1

    SRm= Sj(SRm-1) || Om-1 (m = 2, 3, 4,...., N)

    Om= Fj(EK(SRm)) (m = 2, 3, 4,...., N)

    Cm= Om ⊕ Pm (m = 2, 3, 4,...., N)

    C = C1 || C2 || C3 || .... || CN

  • 解密方式：

    SR1= IV

    O1= Fj(DK(SR1))

    P1= O1 ⊕ C1

    SRm= Sj(SRm-1) || Om-1 (m = 2, 3, 4,...., N)

    Om= Fj(DK(SRm)) (m = 2, 3, 4,...., N)

    Pm= Om⊕Cm (m = 2, 3, 4,...., N)

    P = P1 || P2 || P3 || .... || PN

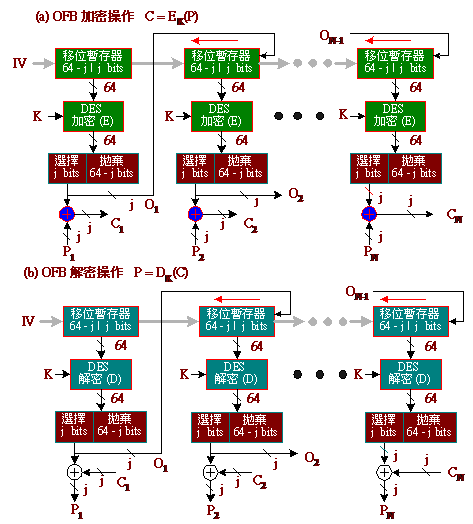    OFB模式DES演算法

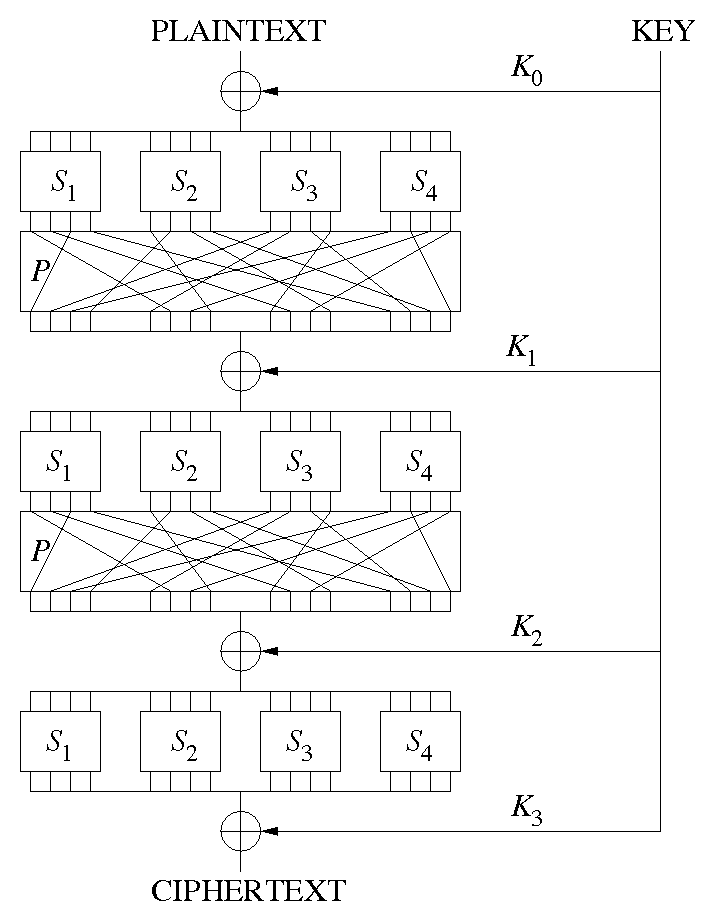
Claude Shannon 與取代-置換網路：

  1. Claude Shannon 在 1949 年提出了取代-排列(S-P)網路的想法，成為當代區塊加密法的基礎。
  2. S-P 網路是以下列兩種基本密碼學運算為基礎：取代 (Substitution-box)與置換 (Permutation-box)。

簡略表示的SPN演算法變種，其中包括三輪加密，使用多個S盒和P盒，加密16位元的明文區塊到等長密文區塊。S盒由Si表示，P盒由P表示，輪金鑰為Ki。

DES與Feistel密碼：

美國國家標準局(National Bureau of Standard, NIST前身)於1973年公開招募密碼演算法，已制定美國國家標準，由IBM研發的一種叫作Lucifer的對稱式金鑰密碼系統，經美國國家標準局交由美國國家安全局(NSA)修訂，成為資料加密標準(DES)，廣泛使用數十年。如台灣一般健保IC卡，其中加密系統所用之對稱式金鑰密碼就是Triple DES。DES密碼是符合70年代早期電腦硬體的規格，主要是用到簡易運算，如二元運算XOR、循環位移(Cyclic Shift)及置換取代等。

DES在密碼學發展歷史中，是第1個由其研發者主動公開其演算法的密碼系統，其主要架構是源自一種所謂Feistel密碼的想法，在此先就Feistel密碼來討論。

Feistel密碼(Feistel Cipher)：

  • Horst Feistel在美國IBM工作期間完成了此項開拓性研究。通常也稱為Feistel network。大部分區塊加密使用該方案，包括DES。Feistel結構的優點在於加密和解密操作非常相似，在某些情況下甚至是相同的，只需要逆轉金鑰編排方式。因此，實現這種密碼所需的代碼或電路大小能幾乎減半。

  • Feistel network最初在IBM的Lucifer對稱式密碼系統中商業化。

  • Feistel Cipher重要特點：

    1. 加密與解密都是相同的編碼器，也就是明文經由編碼器處理後，則輸出為密文；密文再經過編碼器處理後，即還原明文。

    2. 回合函數(Round Function)F有取代加密的功能，越複雜則明文與密文之間的複雜度越高，回合函數F越複雜，由密文猜測出明文越困難。

    3. 它將所欲編碼的資料(64 bits)分割成兩群：右邊(R, 32 bits)與左邊(L, 32 bits)，再交叉移位，因此也具有移位加密的功能。

  • 實踐Shannon的取代-置換網路的概念。

  • 與取代-置換網路相比，Feistel的一個優點是回合函數F不必是可逆的。

  • Feistel Cipher的設計原理：

    1. 區段大小(block size)：增大區塊可以提升安全性，但是加解密會變慢。

    2. 金鑰長度(key size)：增加長度可以提升安全性，使得暴力搜尋金鑰變得更困難，但是加解密會變慢。

    3. 回合數(number of rounds)：增加回合數可以提升安全性，但是加解密會變慢。

    4. 子金鑰的產生(subkey generation)：複雜的產生方法可以使分析變困難，但是加解密會變慢。

    5. 回合函數(round function)：複雜的函數可以使分析變困難，但是加解密會變慢。

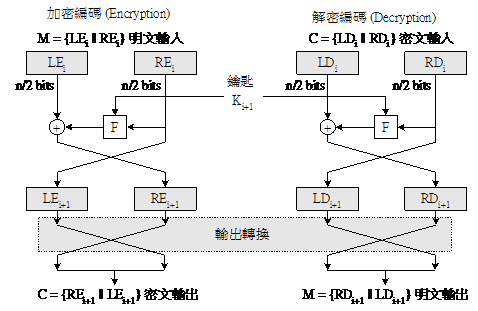    Feistel密碼加密與解密一回合

  • 加密方式：
    明文輸入：M = {LEi|| REi}

    LEi+1=REi

    REi+1= LEi ⊕ F(Ki+1，REi)

    密文輸出：C = {REi+1|| LEi+1} = { LEi ⊕ F(Ki+1，REi) || REi}

  • 解密方式：
    密文輸入：C = {LDi || RDi}

    LDi+1= RDi

    RDi+1= LDi ⊕ F(Ki+1，RDi)

    LDi= REi+1

    RDi= LEi+1

    則Feistel解碼器輸出為：

    LDi+1= RDi = LEi+1= REi

    RDi+1= LDi ⊕ F(Ki+1，RDi) = REi+1 ⊕ F(Ki+1，LEi+1) = LEi ⊕ F(Ki+1，REi) ⊕ F(Ki+1，REi)

    = LEi⊕0 (因為：A ⊕ A = 0)

    = LEi (因為：A ⊕ 0 = A)

  • Feistel密碼系統架構：

    • Feistel的構想是如能利用上圖的加密程序，重複運算幾次，並且每一次都給予不同的子鑰匙，便能完全打散資料的關聯性，達到複雜加密的效果。

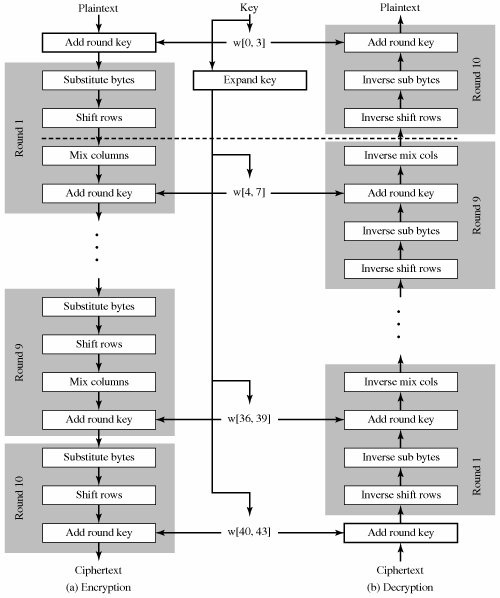
    • 下圖為Feistel密碼系統的架構圖，我們將重複加密的次數(假設16次)，以相同的加密塊連結畫出來；如此，就可以看出明文是經過多個加密塊連續的運算出密文來。值得一提的是，加密與解密均使用同樣的演算法，但子鑰匙分配的次序顛倒。

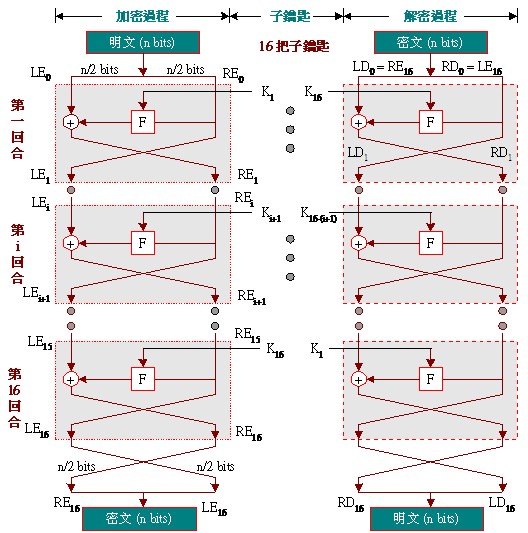
資料加密標準(DES)：

  • DES演算法的製作原理大多來自Feistel架構，它的特性如下：

    1. 鑰匙長度：56 bits(主鑰匙)。

    2. 區塊長度：64 bits。在DES演算法中，明文與密文區塊的長度都是64 bits。

    3. 重複次數：每個區塊重複經過加密器計算16次，每次計算時使用一把獨立的子鑰匙。

    4. 子鑰匙產生器：主鑰匙經過產生器處理之後，產生16把子鑰匙，每一把子鑰匙的長度為48 bits。

    5. 演算法相容：基本上，加密與解密演算法是相同的，解密時將子鑰匙輸入順序與加密相反即可。

  • DES加密區塊的長度為64 bits，但一般明文資料都會超過64 bits，因此以64 bits為單位，將明文分割為若干個區塊，如果最後不足64 bits，則以"0"補足。所產生的密文與明文長度相同，解密時，如有補足部分再將其刪除。另一方面，DES所用的加密和解密鑰匙的長度也是64位元，但在這64位元主鑰匙之中，有8個位元是同位元檢查碼，是用來檢出錯誤，所以真正用來加密的長度只有56個位元。

  • DES演算法的加密流程：

    1. (明文資料分割)每一區塊M=m1m2....m64(64 bits)。最後區塊如果不足於64 bits，則以"0"補足64 bits。

    2. (子鑰產生)計算16個長度為48 bits之子鑰Ki (i=1, 2, ....,16)。

      產生方法：

      • 將 56 bits 分成兩組 28 bits (C0 與 D0)。

      • 左旋運算子 (LSi)。

      • Ci = LSi(Ci-1)。

      • Di = LSi(Di-1)。

      • Ki = PC-2(Ci || Di) (i = 1, 2, 3, ...., 16)。

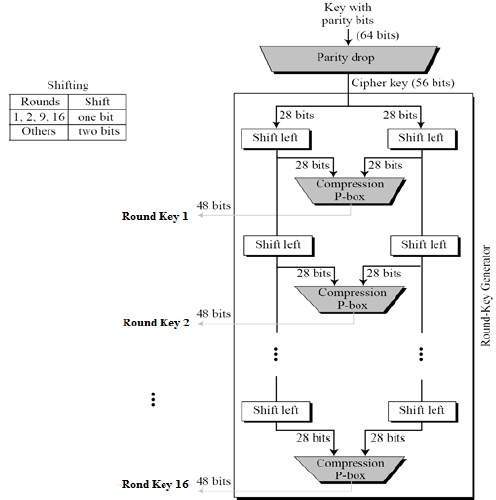        SubKey Generation

        PC1 = Parity drop and PC2 = Compression P-box

    3. (初始置換，Initial Permutation, IP)類似移位功能。

      初始置換與終結置換表

      (L0, P0) = IP(M)，

      L0 = m58m50....m8，

      R0 = m57m49....m7。

    4. 選擇子鑰Ki，共有16把子鑰，每一把鑰匙的長度是48 bits，並開始Feistel加密重複16次，每次使用不同的子鑰加密。

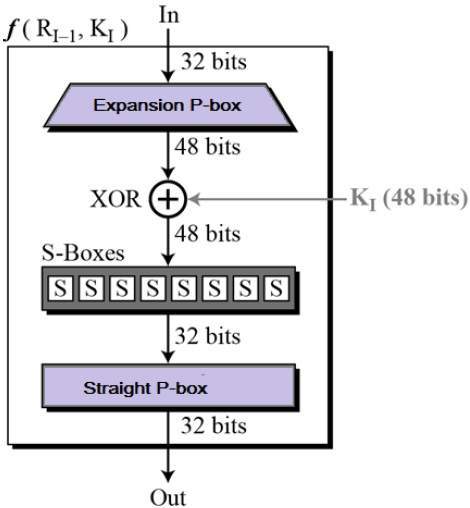      DES 的 f函數

      Li = Ri-1，

      Ri = Li-1 ⊕ f(Ri-1, Ki)，

      f(Ri-1, Ki) = P(S(E(Ri-1) ⊕ Ki)) (i=1, 2, ...., 16)。

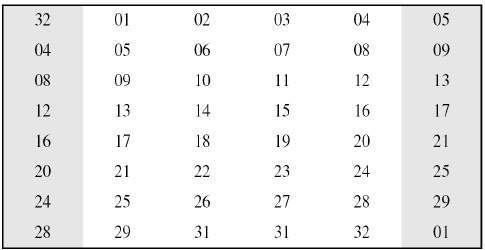      E(Ri-1)擴充函數(Expansion P-box)

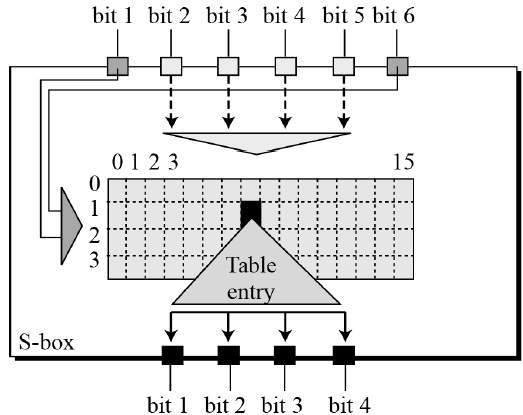      DES S-box rule

      S-box Table

      S-box輸入為6 bits，輸出為4 bits，在1970年代已是一個晶片最大容量，這已是當年技術之極限。

      S-box為DES演算法之核心，本身為非線性函數，與古典密碼大多採用線性函數有相當大的差別，為DES密碼安全性保證的關鍵。IBM在設計S-box時，早就已經預先預防某些特定攻擊法，如差分攻擊法(Differential Cryptanalysis)。

      Straight P-box

    5. 最後一回合對應至(R16, L16) = b1b2....b64。

    6. C = IP^-1(b1b2....b64)，其中IP^-1即為IP之反函數。

Advanced Encryption Standard, AES：

  • 在AES出現之前，大多是用多次的DES加密來處理。為了取代DES，NIST在1997年公布AES (Advanced Encryption Standard，高等加密標準) 徵選活動。

  • 在2000年10月，NIST宣佈來自比利時的兩位密碼學家 － Joan Daemon和Vincent Rijmen，他們提出的Rijndael演算法贏得這項競賽。並於2001年11月完成評估，發佈為FIPS PUB 197標準。

  • AES牢靠度高、適用於高速網路、可在硬體設備建置等因素，都是這個演算法獲選的原因。

  • AES的特色：

    • 採用對稱式區塊加密法。

    • 資料區塊為128位元，金鑰為 128、192、256 位元。

    • 運算速度比Triple-DES更強更快。

    • Rijndael的編碼架構是不再使用Feistel Cipher而是採用「迭代式區塊加密」(Iterated Block Cipher, IBC)。IBC是將各區塊以陣列格式排列，以位元組(Byte)為單位，陣列之間反覆排列與取代來達到編碼的目的。

  • Rijndael的設計原理與DES有很大的不同，在計算上，是採用Galois體GF(2^8)之算數為計算之基礎，藉由強韌乾淨的代數運算，建構乘難破解，卻能加速加解密的演算法。

  • Rijndael演算法是利用3個參數決定加密與解密的處理架構，而其中一個參數是由另兩個參數演變而來的，如下說明：

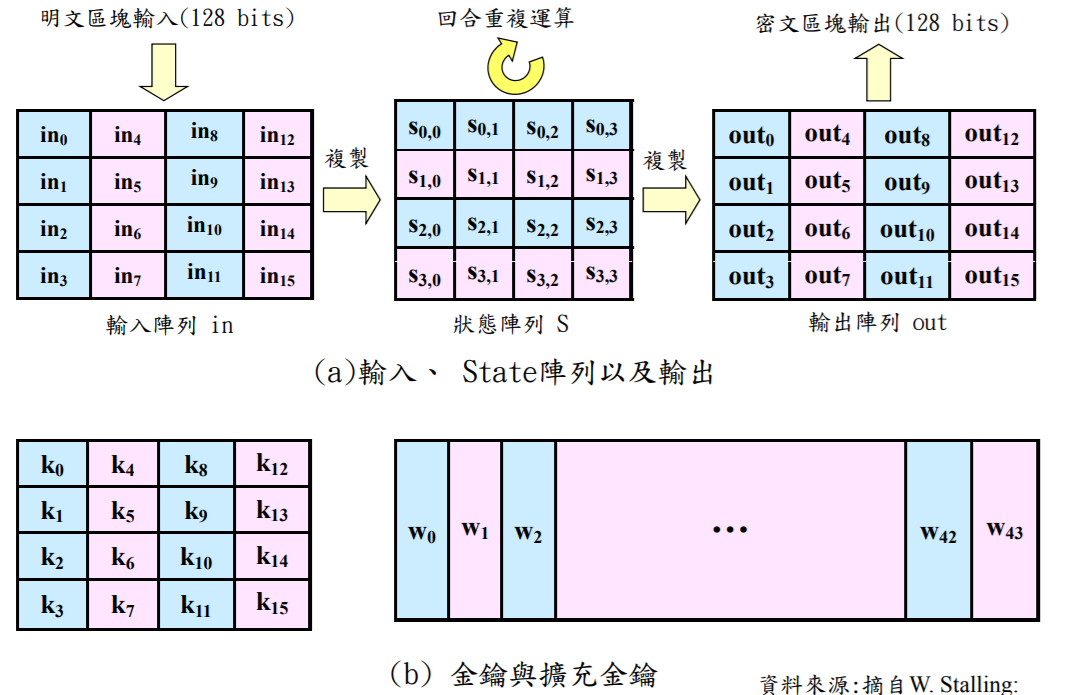
    1. 明文區段數目(Nb)：表示32 bits加密區段的數目，此參數為輸入的明文區塊可區分為多少個加密區段，以AES標準而言，輸入明文區塊為128 bits，因此可區分為四個加密區段(Nb= 4)。

    2. 金鑰區段數目(Nk)：此參數為加密金鑰可區分為多少個金鑰區段，每一區段的大小也是32 bits。如AES-128，則Nk= 4；AES-192，則Nk= 6；而AES-256，則Nk= 8。

    3. 重覆次數(Nr)：此參數表示加密(或解密)編碼所需重覆的次數。到底需要重覆幾次，這與明文以及金鑰的複雜度有關，必須取捨兩者之間較複雜的作為重覆次數的依據；也就是說，取明文與金鑰之間較長者(或稱區段數目較多者)，作為重覆次數的標準，如此，才能將資料(明文或鑰匙)完全的混合，此為Rijndael演算法較特殊的地方，計算方式為：Nr= 6 + max(Nb, Nr)。

明文區段Nb 金鑰區段Nk 回合次數Nr
AES-128 4 4 10
AES-192 4 6 12
AES-256 4 8 14

  • AES之基本單位：

    AES-128之區塊大小為128-bit，可分為16個byte，即狀態矩陣(State Matrix)S=(s00, s10, s20, s30, s01, s11, ...., s33)，配置成係數為GF(2^8)之4x4矩陣。

    其中每個byte sij為GF(2^8)元素，Rijndael之GF(2^8)採模型：GF(2^8) ≈ GF(2)[x] / (x^8+x^4+x^3+x^1+1)，矩陣中的行向量(Column Vector)會對應至GF(2^8)為係數的多項式。

  • AES-128演算法主要可分為四大運算：

    1. SubByte

    2. ShiftRow

    3. Mixcolumn

    4. AddRoundKey

    加密演算法如下：

    Cipher (byte in[4*Nb], byte out[4*Nb], word w[Nb*(Nr+1)])

/* in 為輸入陣列、out = 輸出陣列、w = 鑰匙字元陣列 */

Begin

Byte state[4, Nb]

/* 明文陣列複製到狀態陣列上 */

state = in

/* 第 0 回合編碼 */

AddRoundKey(state, w[0, Nb-1])

/* 第 1 到 Nr – 1 回合編碼 */

for round = 1 step 1 to Nr-1

SubBytes(state)

ShiftRows(state)

MixColumns(state)

AddRoundKey(state, w[round*Nb, (round+1)*Nb-1])

end for

/* 第 Nr回合編碼 */

SubBytes(state)

ShiftRows(state)

AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1])

/* 密文陣列輸出 */

out = state

end

  • SubByte：

    • 在Rijndael演算法有兩種S-Box使用，一種在加密，另一種在解密，互為反運算，即SubByte以及InverseSubByte，均可用代數方式來描述。

    • Rijndael狀態矩陣中任一byte s=[s7,s6,s5,....,s0]均視為GF(2^8) ≈ GF(2)[x] / (x^8+x^4+x^3+x^1+1)之元素，即s=s7x^7+s6x^6+...+s0。

    • 計算如下：

      1. 若s=0，則x=0，否則計算在GF(2)[x] / (x^8+x^4+x^3+x^1+1)中s之乘法反元素，即以廣義輾轉相除法得x=s^-1。x=[x7,x6,x5,...,x0]。

      2. 計算仿射函數(Affine Mapping)：

      3. 得到y=[y7,y6,y5,...,y0]為經過SubByte作用之值。

    • 雖然SubByte與InverseSubByte都有良好的代數描述，在實用上，還是採用S-Box除了可加快速度外，又可以抵擋相當程度的時序攻擊。

      範例：以s=x^7+x^6+x^3+x+1∈GF(2^8) ≈ GF(2)[x] / (x^8+x^4+x^3+x^1+1)為例

      s=x^7+x^6+x^3+x+1 => (11001011)=0xCB

      由AES S-Box會對應到(C,B)項，即y=0x1F=(00011111) => x^4+x^3+x^2+x+1

  • ShiftRow and MixColumn：

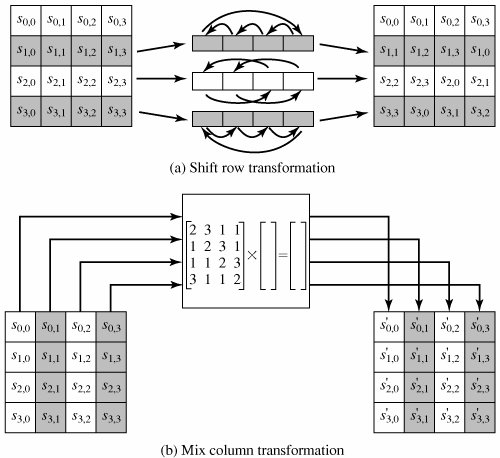
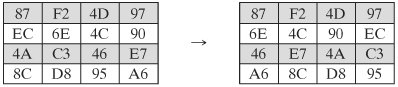    ShiftRow範例

    Rijndael狀態矩陣每一行向量，可視為3次GF(2^8)多項式：a(X)=a0+a1X+a2X^2+a3X^3，

    乘上多項式c(X) (mod X^4+1)：c(X)=0x02+0x01X+0x01X^2+0x03X^3 (mod X^4+1)。

    此運算等價於：。

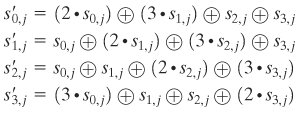
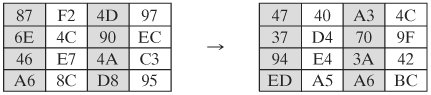    MixColumn範例

    s'00 = ({02} · {87}) ⊕ ({03} · {6E}) ⊕ {46} ⊕ {A6} = {47}

    s'10 = {87} ⊕ ({02} · {6E}) ⊕ ({03} · {46}) ⊕ {A6} = {37}

    s'20 = {87} ⊕ {6E} ⊕ ({02} · {46}) ⊕ ({03} · {A6}) = {94}

    s'30 = ({03} · {87}) ⊕ {6E} ⊕ {46} ⊕ ({02} · {A6}) = {ED}

    而InverseMixColumn為MixColumn之反運算，即左乘上述4x4矩陣之反矩陣：

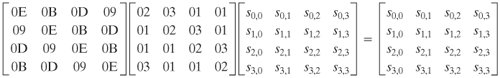
  • AddRoundKey：

    • 將狀態矩陣與回合子鑰進行XOR運算，即：

      第一個矩陣為狀態矩陣，第二個為子鑰矩陣。

    • 在AES-128演算法尚需從128-bit金鑰K產生11回合子鑰k[0],k[1],k[2],....k[10]。

      AES之金鑰擴充

      RotWord：循環左移1個byte，如 [b0, b1, b2, b3] 會變成 [b1, b2, b3, b0]。

      SubWord：依照上述之AES S-Box來取代。

      Rcon(Round Content)：將RotWord和SubWord運算結果和Rcon運算結果進行XOR。

      Rcon[j] = (RC[j], 0, 0, 0), with RC[1] = 1, RC[j] = 2 · RC[j - 1] and with multiplication defined over the field GF(2^8). The values of RC[j] in hexadecimal are：

      | j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | RC[j] | 01 | 02 | 04 | 08 | 10 | 20 | 40 | 80 | 1B | 36 |

    • 範例：假設第8回盒子鑰 EA D2 73 21 B5 8D BA D2 31 2B F5 60 7F 8D 29 2F

      則第9回盒子鑰為：

      | i (decimal) | temp | After RotWord | After SubWord | Rcon (9) | After XOR with Rcon | w[i-4] | w[i] = temp ⊕ w[i-4] | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | 9*4=36 | 7F8D292F | 8D292F7F | 5DA515D2 | 1B000000 | 46A515D2 | EAD27321 | AC7766F3 |

results matching ""

    No results matching ""